Through Mazes to Mathematics

Exponential growth: I(n+4) >= 8I(n)


I(n) represents the number of interesting n-level mazes: those whose level sequence does not begin with 01... nor end with ...n-1,n.

If n is an even number, then each n-level interesting maze gives rise to eight distinct (n+4)-level interesting mazes, which are different from the mazes constructed by this process from any other n-level interesting maze. Their paths are illustrated in this figure, where the part of the path inside the box is the original n-level maze.


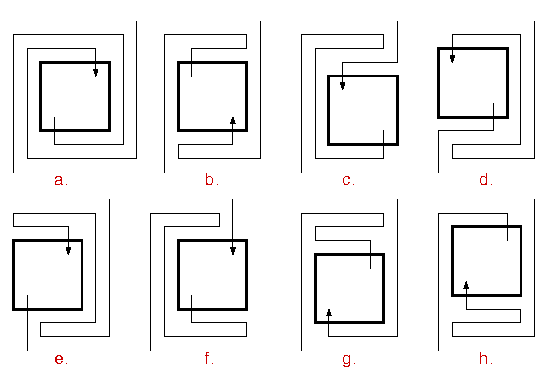
Each interesting n-level maze gives rise to 8 different interesting mazes of depth n+4; in b,g,h the path runs through the n-level maze backwards.

To see why, let s be the permutation of 0,...,n that gives the level sequence of the original maze as

0, s1, . . . , sn-1, n.

Then the illustrated mazes have level sequences:

a.  0, n+3,   2, s1+2, .     .    .     , sn-1+2, n+2, 1,  n+4

b.  0, n+3, n+2, sn-1+2,     .     .     .  , s1+2, 2, 1,  n+4

c.  0,  3, s1+3,   .     .     .     , sn-1+3, n+3, 2, 1,  n+4

d.  0, n+3, n+2,   1,  s1+1,  .    .     .  , sn-1+1, n+1, n+4

e.  0, n+3, n+2,   1,    2, s1+2,   .    .   .   , sn-1+2, n+4

f.  0, s1+2,    .    .    .    ,   sn-1+2, n+2, n+3, 2, 1, n+4

g.  0, n+3, sn-1+3,    .     .    .     ,   s1+3, 3, 2, 1, n+4
 
h.  0, n+3, n+2,  n+1, sn-1+1,   .   .    .     , s1+1, 1, n+4

The verification that these sequences are all distinct can be done in a table, where the (x,y) entry gives one place where (at least) the level sequences of mazes x and y must differ. * means that the ``interesting'' condition is invoked (it means here that s1 is not 1, nor is sn-1 equal to n-1.)

    a  b  c  d  e  f  g  h

a      2  1  2  2  2  2  2

b         1  3  3  1  2* 3*

c            1  1  1* 1  1

d               4* 1  3  3

e                  3  3  3

f                     1  1

g                        2*
Note that this argument does not use any property of the permutation s except that it is interesting. It follows that for one of the eight mazes derived from a different interesting permutation t to be equal to one of those coming from s, they would both come from the same pattern, say a. But that can only happen if t = s.

Return to How did I get interested ...

Return to Main Maze Page

Return to Tony's Home Page

Tony Phillips
Math Dept SUNY Stony Brook
tony@math.sunysb.edu
April 2 1999