| > | R:=0.3:
xphug:= [ diff(theta(t),t) = ( v(t)^2 - cos(theta(t))) / v(t), diff(v(t),t) = -sin(theta(t)) - R*v(t)^2 , diff(x(t),t) = v(t)*cos(theta(t)), diff(y(t),t) = v(t)*sin(theta(t))]; |
| (1) |
| > | with(DETools):with(plots): |
| > |
| > |
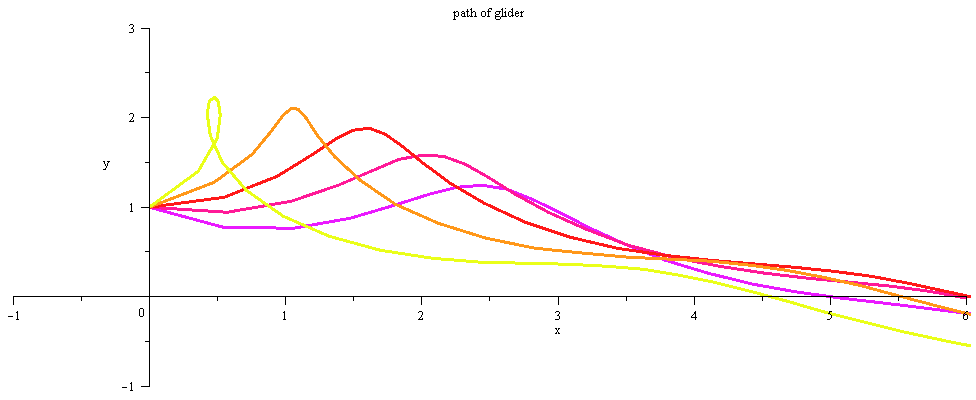
DEplot(xphug, [ theta(t), v(t), x(t), y(t) ], t=0..15, |
| > | [seq([theta(0)=(Pi*(i/10)), v(0)=2, x(0)=0, y(0)=1 ], i=-2..2)], |
| > | theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=-1..3,
scene=[x,y], title="path of glider", |
| > | linecolor=[seq(COLOR(HUE,i/11),i=-2..2)]);
|
| > |
 |
| > | R:=0.3:
motorphug:= [ diff(theta(t),t) = ( v(t)^2 - cos(theta(t))) / v(t), diff(v(t),t) = -sin(theta(t)) - R*v(t)^2 +k, diff(x(t),t) = v(t)*cos(theta(t)), diff(y(t),t) = v(t)*sin(theta(t))]; |
| (2) |
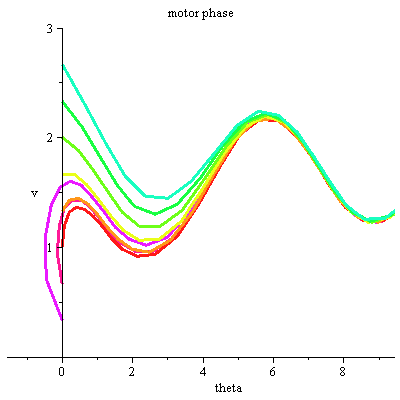
| > | k:=1;DEplot(motorphug, [ theta(t), v(t), x(t), y(t) ], t=0..15, |
| > | [seq([theta(0)=0, v(0)=1+i/3, x(0)=0, y(0)=1 ], i=-5..5)], |
| > | theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=-1..3,
scene=[theta,v], title="motor phase", |
| > | linecolor=[seq(COLOR(HUE,i/11),i=-5..5)]); |
| > |
| Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution past the initial point, problem may be complex, initially singular or improperly set up |
|
 |
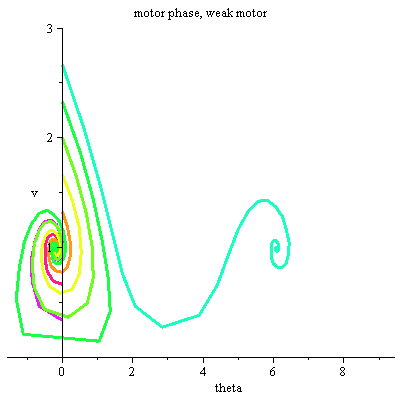
| > | k:=0.1;DEplot(motorphug, [ theta(t), v(t), x(t), y(t) ], t=0..15, |
| > | [seq([theta(0)=0, v(0)=1+i/3, x(0)=0, y(0)=1 ], i=-5..5)], |
| > | theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=-1..3,
scene=[theta,v], title="motor phase, weak motor", |
| > | linecolor=[seq(COLOR(HUE,i/11),i=-5..5)]); |
| > |
| Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution past the initial point, problem may be complex, initially singular or improperly set up |
|
 |
| > | ? |
| > | sol:=dsolve({op(xphug), theta(0)=0, v(0)=2, x(0)=0, y(0)=1},
numeric, range=0..1); |
| (3) |
| > | sol(5); |
| (4) |
| > | sol(6); |
| (5) |
| > | sol(7); |
| (6) |
| > | sol(8); |
| (7) |
| > | sol(7.5); |
| (8) |
| > | sol(7.25); |
| (9) |
| > | sol(7.125); |
| (10) |
| > | sol(7.1); |
| (11) |
| > | sol(7.05); |
| (12) |
| > | yt:= T->subs(sol(T), y(t)); |
| (13) |
| > | yt(7.02); |
| (14) |
| > | bisector := proc( f, low, high, epsilon)
local mid, lo, hi; lo := low; hi := high; mid := (lo+hi)/2; while ( abs(f(mid))>epsilon) do if ( f(mid) > 0) then hi:= mid; else lo:= mid; fi; mid := (lo+hi)/2; od; return(mid); end: |
let's test it for something we know the answer.
| > | bisector(2*x-1, 0, 1, 0.001); |
| Error, (in bisector) cannot determine if this expression is true or false: 0.1e-2 < abs(2*x(1/2)-1) |
| > | bisector(2*x-1, 0, 5, 0.001); |
| Error, (in bisector) cannot determine if this expression is true or false: 0.1e-2 < abs(2*x(5/2)-1) |
| > | bisector(x->2*x-1, 0, 5, 0.001); |
| (15) |
| > | evalf(%); |
| (16) |
Ramon prefers decimals
| > | bisector := proc( f, low, high, epsilon)
local mid, lo, hi; lo := evalf(low); hi := evalf(high); mid := evalf((lo+hi)/2); while ( abs(f(mid))>epsilon) do if ( f(mid) > 0) then hi:= mid; else lo:= mid; fi; mid := (lo+hi)/2; od; return(mid); end: |
| > | bisector(x->x^2-1, 0, 5, 0.001); |
| (17) |
| > | bisector(yt, 8, 7, 0.00001); |
| (18) |
| > | yt(7.081542969); |
| (19) |
| > | bisector := proc( f, low, high, epsilon)
local mid, lo, hi; lo := evalf(low); hi := evalf(high); mid := evalf((lo+hi)/2); while ( abs(f(mid))>epsilon) do if ( f(mid) > 0) then hi:= mid; else lo:= mid; fi; mid := (lo+hi)/2; print( [lo, hi], mid, "f(mid)=", f(mid)); od; return(mid); end: |
| > | bisector(yt, 8, 7, 0.001); |
| (20) |
Don't try this at home, kids!
it runs forever and is hard to interrupt.
| > | # bisector(yt, 7, 8, 0.001); |
| Warning, computation interrupted |
| > | bisector := proc( f, low, high, epsilon)
local mid, lo, hi; lo := evalf(low); hi := evalf(high); if (abs(f(lo))>0) then error("f not neg at lo=",lo); fi; if (abs(f(hi))>0) then error("f not pos at hi=",hi); fi; mid := evalf((lo+hi)/2); while ( abs(f(mid))>epsilon) do if ( f(mid) > 0) then hi:= mid; else lo:= mid; fi; mid := (lo+hi)/2; print( [lo, hi], mid, "f(mid)=", f(mid)); od; return(mid); end: |
| > | bisector(yt, 7, 8, 0.001); |
| Error, (in bisector) f not neg at lo=, 7. |
| > |