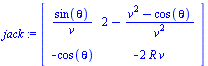
>	jack := VectorCalculus[Jacobian](    [  (v^2 - cos(theta))/v, -sin(theta) - R*v^2 ],  [theta, v]);

 

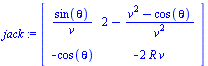(1)

 

>	fix:=convert(  solve( { -sin(theta) - R*v^2 = 0, (v^2 - cos(theta))/v =0 }, {theta,v}),  radical);

 

(2)

 

>	eval(jack, fix);

 

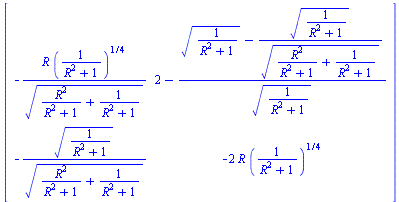(3)

 

>	simplify(eval(jack, fix));

 

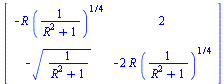(4)

 

>	eval(%,R=0);

 

(5)

 

>	jill := unapply( simplify(eval(jack, fix)), R):

 

>	jill(0); jill(R); jill(0.2);

 

 

 

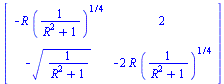	(6)

 

>	with(LinearAlgebra):

 

>	Eigenvalues(jill(0.2));

 

(7)

 

>	[Trace(jill(0.2)), Determinant(jill(0.2)) ];

 

(8)

 

for what R is tr^2 = 4*det? 

>	discr := Trace(jill(R))^2 - 4*Determinant(jill(R));

 

(9)

 

>	solve(discr=0, R);

 

(10)

 

>	evalf(eval(discr,R=2*sqrt(2)+.1));

 

(11)

 

>	evalf(eval(discr,R=2*sqrt(2)-.1));

 

(12)

 

>	evalf(eval(discr,R=100));

 

(13)

 

>	evalf(jill(100));

 

(14)

 

>	Determinant(jill(100));

 

(15)

 

>	Determinant(jill(R));

 

(16)

 

>	R:='R': xphug:= [ diff(theta(t),t) = ( v(t)^2 - cos(theta(t))) / v(t),         diff(v(t),t)     = -sin(theta(t)) - R*v(t)^2 ,         diff(x(t),t)     = v(t)*cos(theta(t)),         diff(y(t),t)     = v(t)*sin(theta(t))];

 

(17)

 

>	with(DETools):with(plots):

 

>	R:=1; display( array([      DEplot(xphug, [ theta(t), v(t), x(t), y(t) ], t=0..10,

 

>	[[theta(0)=0, v(0)=2.5, x(0)=0, y(0)=4 ],           [theta(0)=0, v(0)=.8,  x(0)=0, y(0)=1 ]],

 

>	theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=0..7,         scene=[theta,v],

 

>	linecolor=[blue,red], stepsize=0.1, title="v,theta phase"),

 

>	DEplot(xphug, [ theta(t), v(t), x(t), y(t) ], t=0..10,

 

>	[[theta(0)=0, v(0)=2.5, x(0)=0, y(0)=4 ],           [theta(0)=0, v(0)=.8,  x(0)=0, y(0)=1 ]],

 

>	theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=0..7,         scene=[x,y], title="path of glider",

 

>	linecolor=[blue,red], stepsize=0.1)       ]));

 

>

 

>	eval(fix);

 

(18)

 

>	R:=3; display( array([      DEplot(xphug, [ theta(t), v(t), x(t), y(t) ], t=0..10,

 

>	[[theta(0)=0, v(0)=2.5, x(0)=0, y(0)=4 ],           [theta(0)=0, v(0)=.8,  x(0)=0, y(0)=1 ]],

 

>	theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=0..7,         scene=[theta,v],

 

>	linecolor=[blue,red], stepsize=0.1, title="v,theta phase"),

 

>	DEplot(xphug, [ theta(t), v(t), x(t), y(t) ], t=0..10,

 

>	[[theta(0)=0, v(0)=2.5, x(0)=0, y(0)=4 ],           [theta(0)=0, v(0)=.8,  x(0)=0, y(0)=1 ]],

 

>	theta=-Pi/2..3*Pi, v=0..3, x=-1..6, y=0..7,         scene=[x,y], title="path of glider",

 

>	linecolor=[blue,red], stepsize=0.1)       ]));

 

>

 

>	Eigenvectors(jill(3.0)); evalf(fix);

 

 

	(19)

 

>