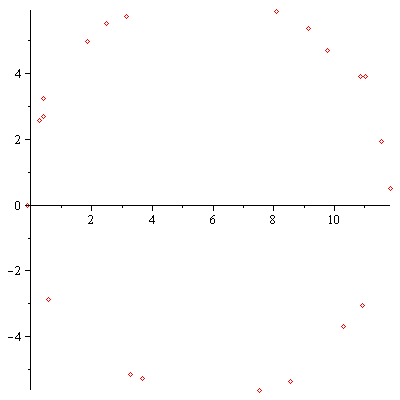
>	read("/home/scott/www/mat331.spr08/problems/lsq_data.txt");

 

defined line_pts(), bad_line_pts(), quadratic_pts(), cubic_pts(), and circle_pts()

 

>	cdat:=circle_pts():

 

>	plot(cdat,style=point);

 

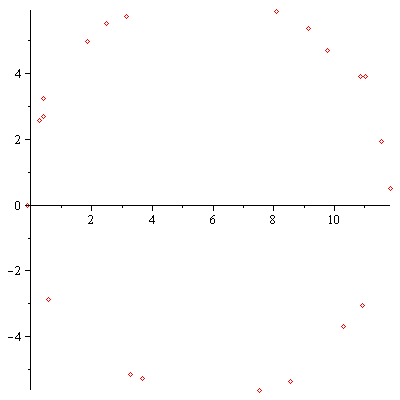Idea:  Let's define the distance from [ to circle centered (a,b), radius r by  ( (x-a) 

>	epsilon:=(a,b,r,pt) -> (a-pt[1])^2 + (b-pt[2])^2 - r^2;

 

(1)

 

Now minimize sums of squares of that. 

>	E:=(a,b,r,data) -> sum( (epsilon(a,b,r,data[i])^2), i=1..nops(data));

 

(2)

 

>	E(6,0,7,cdat);

 

(3)

 

>	E(6,0,6,cdat);

 

(4)

 

>	diff(E(a,b,r,cdat),a);

 

(5)

 

>	crits:=solve( { diff(E(a,b,r,cdat),a)=0, diff(E(a,b,r,cdat),b)=0, diff(E(a,b,r,cdat),r)=0},        {a,b,r});

 

(6)

 

The 6th answer is reasonable, the others are crazy. 

>

crits[6];

 

(7)

 

>	subs(crits[6], r);

 

(8)

 

>	subs(crits[4], r);

 

(9)

 

>	select( h -> subs(h,r) > 0, crits);

 

Error, selecting function must return true or false

 

>	select( h -> if (subs(h,r) > 0) then true else false fi, crits);

 

Error, (in unknown) cannot determine if this expression is true or false: 0 < r

 

>	checkit:= s-> if (subs(s,r) > 0) then true else false fi;

 

(10)

 

>	checkit(crits[3]);

 

(11)

 

>	select( checkit, {crits});

 

(12)

 

>	mysol:=op(select( checkit, {crits}));

 

(13)

 

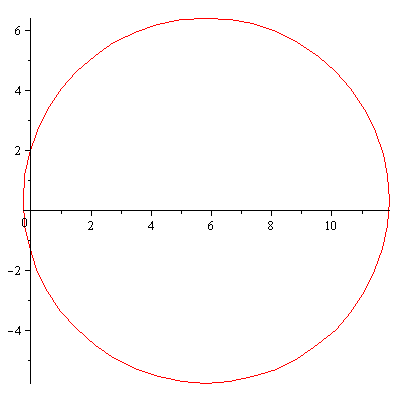
>	mycircle:= subs(mysol, [a+r*cos(t),b+r*sin(t)]);

 

(14)

 

>	mycircle:= subs(mysol, [a+r*cos(t),b+r*sin(t), t=0..2*Pi]);

 

(15)

 

>	plot(mycircle,scaling=constrained);

 

>	plots[display]( [plot(mycircle,color=blue), plot(cdat,style=point,color=green)]);

 

>
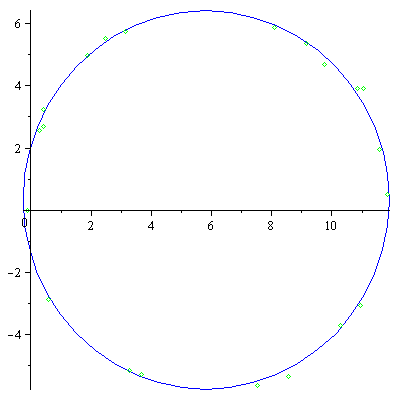