>	data := [[6.399555221, -2.975032259], [.972268069, 4.644979231], [-.174930733,

 

>	2.313538498], [-5.073540384, 9.514984401], [6.893861527, -1.071097006], [1.510\

 

>	235158, 4.569017281], [.955599370, 4.097468044], [-5.712634201, 9.544519402],

 

>	[.691425053, 3.830846574], [-6.708865618, 9.962202300], [3.761176009, 1.978739\

 

>	404], [3.172070319, .432025264], [-2.684165704, 7.561362842], [-4.250626903, 8\

 

>	.100249035], [.201116234, 3.609631780], [5.514142588, -.466174813], [4.7227219\

 

>	45, 1.119994312], [7.636264182, -3.679228223], [-4.873069134, 7.999031928], [-\

 

>	5.019405423, 8.742503689], [4.811048112, -.901298665], [-.504420785, 6.1024543\

 

>	05], [6.576501459, -3.495854902], [-.796916715, 3.623549343], [1.325774350, 2.\

 

>	186174499]];

 

>

 

(1)

 

>	plot(data,style=point);

 

>

 

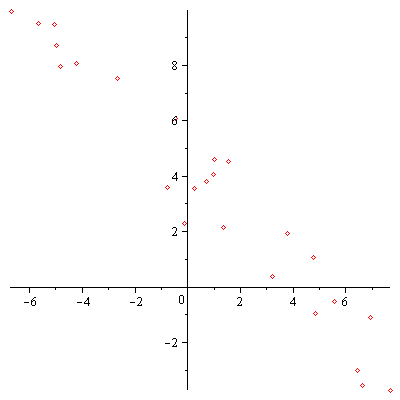>	read( "/home/scott/www/mat331.spr08/problems/proj1data/sandyego.txt");

 

(2)

 

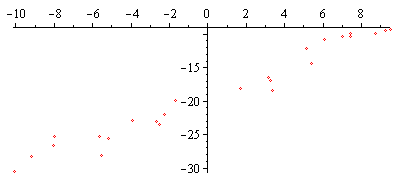
>	plot(data,style=point);

 

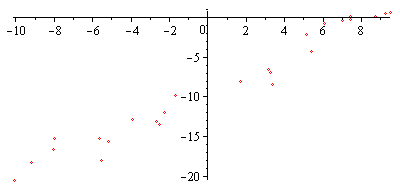
>	data2:= [ seq( [ data[i][1], data[i][2]+10 ], i=1..nops(data) )]:

 

>	plot(data2,style=point);

 

>	save(data2, "/tmp/data2.txt");  # writes out the values of data2 to /tmp/data2.txt as a maple command.

 

>

 

>

 

What directory am I in? 

>	currentdir();

 

(3)

 

Let's change to another. 

>	currentdir("/home/scott/www/mat331.spr08/problems/");

 

(4)

 

>	currentdir();

 

(5)

 

>	currentdir("/home/scott/www/mat331.spr08/problems/"); read("lsq_data.txt");

 

 

defined line_pts(), bad_line_pts(), quadratic_pts(), cubic_pts(), and circle_pts()

 

>	plot(line_pts(), style=point);

 

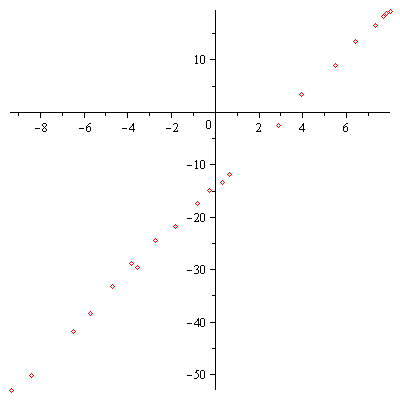>	qdata := quadratic_pts(): plot(qdata, style=point);

 

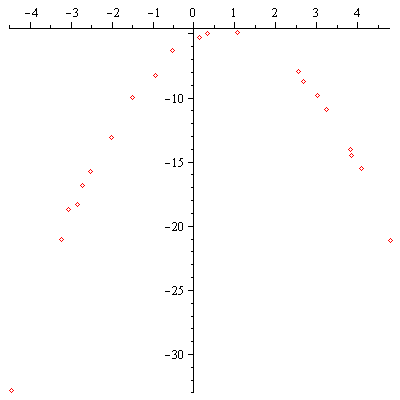>	f:=x->x^3+3;

 

(6)

 

>

f(2);

 

(7)

 

>	g:=proc(x)  x^3+3; end;

 

(8)

 

>

g(2);

 

(9)

 

>	h:=proc(x)  y := x^3;  y+3; end;

 

 

Warning, `y` is implicitly declared local to procedure `h`
	(10)

 

>

h(2);

 

(11)

 

Let's try to fit a quadratic of the form It will be way fun. 

But let's use a more general procedure or "macro" (except it isn't a macro) or subroutine or whatever. 

>	fitquad := proc( data )  local f,dis,ans,i,a,b,c;  f:= x-> a*x^2 + b*x + c;    # distance is sum of squares of f(x)-y  dis:= sum( (f(data[i][1]) - data[i][2])^2 , i=1..nops(data));  ans:= solve( { diff(dis,a)=0, diff(dis,b)=0, diff(dis,c)=0},               {a,b,c}); end:

 

>	myfit:=fitquad(data);

 

(12)

 

>

fitquad := proc( data )  local f,dis,ans,i,a,b,c;  f:= x-> a*x^2 + b*x + c;    # distance is sum of squares of f(x)-y  dis:= sum( (f(data[i][1]) - data[i][2])^2 , i=1..nops(data));  ans:= solve( { diff(dis,a)=0, diff(dis,b)=0, diff(dis,c)=0},               {a,b,c});  assign(ans);  return(f(x)); end:

 

>	qOfX:=fitquad(qdata);

 

(13)

 

>

qOfX(2);

 

(14)

 

>	q:=unapply(qOfX, x);

 

(15)

 

>

q(2);

 

(16)

 

>

q(y);

 

(17)

 

>

fitquad := proc( data )  local f,dis,ans,i,a,b,c,q;  f:= x-> a*x^2 + b*x + c;    # distance is sum of squares of f(x)-y  dis:= sum( (f(data[i][1]) - data[i][2])^2 , i=1..nops(data));  ans:= solve( { diff(dis,a)=0, diff(dis,b)=0, diff(dis,c)=0},               {a,b,c});  assign(ans);  q:=unapply(f(x),x);  return(eval(q)); end:

 

>

 

>	q:=fitquad(qdata);

 

(18)

 

>	plots[display]({plot(qdata,style=point,color=blue),plot(q(x),x=-5..5)});

 

>
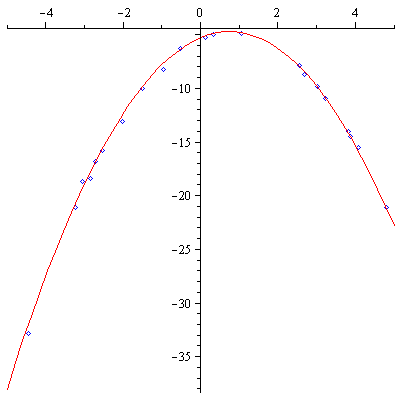