- If it rains, then either I will wear a coat or I'll stay home.
Solution: You needn't translate this to symbols to do this problem, but let me do so to clarify the reasoning. First, let
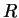 be the statement ``it rains'',
be the statement ``it rains'',
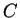 be ``I will wear a coat'', and
be ``I will wear a coat'', and 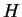 be ``I'll stay home''. Thus, the
negation of the statement is
be ``I'll stay home''. Thus, the
negation of the statement is
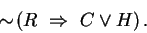
An implication is false (that is, negated) exactly when the hypothesis is true and the conclusion is false,1 so we get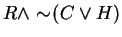 , or equivalently,
, or equivalently,
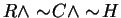 . Translating back to English, we get
. Translating back to English, we get
When it rains, I won't wear a coat and I won't stay home.
or perhaps you might sayI will go out in the rain without a coat.
- This function has no inverse, and it is not continuous.
Solution: This is of the form
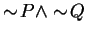 , which is negated as
, which is negated as 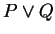 ,
so we get
,
so we get
This function is invertible or it is continuous.
I suppose if you wanted to write this as an implication, you could writeIf this function has no inverse, then it is continuous.
which is equivalent.
- In any triangle, the sum of the measure of the angles is less than
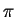 .
.
Solution: Here we have a statement of the form
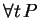 ; the negation of such a
statement is of the form
; the negation of such a
statement is of the form
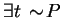 . Thus, we get
. Thus, we get
There is a triangle where the sum of the measure of its angles is at least
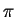 .
.
- For every
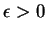 , there is a
, there is a 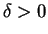 so that
so that
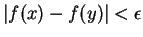 whenever
whenever
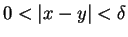 .
.
Solution: This statement is nearly already in symbolic form. The negation is
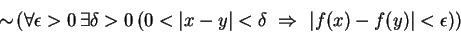
Moving the negation in, we get
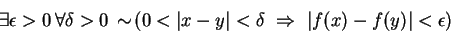
and negating the implication gives
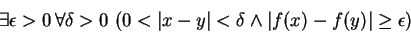
You may recall from calculus that the original statement is the definition of ``The function
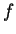 is continuous at the point
is continuous at the point 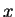 '', so the latter is
``
'', so the latter is
``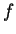 is not continous at
is not continous at 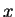 ''.
''.
There is an implied quantifier on the
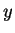 in the statement, that is, it
really should say
in the statement, that is, it
really should say
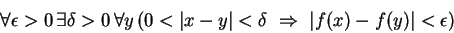
and so the negation would be
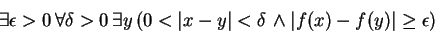
But I didn't write it that way, and I can't expect you to see the implicit quantifier on . Anyway, this course isn't MAT 319 or MAT 320, so let's
not worry about it.
. Anyway, this course isn't MAT 319 or MAT 320, so let's
not worry about it.
- Every natural number has a unique additive inverse.
Solution: The negation is clearly
Not every natural number has a unique additive inverse.
orThere is a natural number which does not have a unique additive inverse.
But we can elaborate further. If a number
 does not have a unique
inverse, either it doesn't have an inverse at all, or it has more than
one.2
So, we have
does not have a unique
inverse, either it doesn't have an inverse at all, or it has more than
one.2
So, we have
There is a natural number which has no additive inverse, or there is a natural number with more than one additive inverse.
As usual, we say
- For every integer
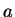 and every integer
and every integer 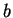 ,
, 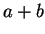 is positive and
is positive and
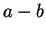 is negative.
is negative.
Solution: This is false. Consider
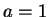 and
and 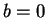 . Then
. Then 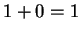 , which is positive,
but
, which is positive,
but 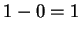 , which is not negative.
, which is not negative.
Since we are insisting that everything be proven with reference to axioms, we probably should work a little harder to fully justify all of our statements. (On an exam, I probably would give nearly full credit for the above counterexample alone. But this isn't an exam, so I should be complete.)First we know that
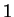 and
and 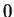 exist, as consequences of axioms V.8 and V.9,
and the fact that
exist, as consequences of axioms V.8 and V.9,
and the fact that 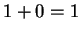 follows immediately from axiom V.8. But, we have not
shown that
follows immediately from axiom V.8. But, we have not
shown that 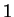 is positive, nor have we shown that
is positive, nor have we shown that 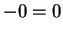 .
.
One way to see that
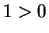 is to use axiom VI.1 (
is to use axiom VI.1 (
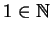 ), but
perhaps this is a bit of a cheat, because we didn't define ``positive'' in
that way.
), but
perhaps this is a bit of a cheat, because we didn't define ``positive'' in
that way.
So let's prove
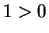 by contradiction.
by contradiction.
Suppose not. Then either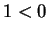 or
or 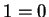 . But
. But 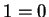 contradicts
axiom V.12.
contradicts
axiom V.12.
If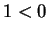 , then
, then 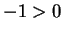 (see the Lemma below). Then applying axiom V.12
(with
(see the Lemma below). Then applying axiom V.12
(with 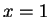 ,
, 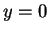 , and
, and 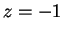 ), we get
), we get
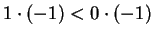 . But this
says
. But this
says 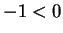 , contradicting the earlier statement. Hence,
, contradicting the earlier statement. Hence, 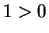 , that is,
, that is, 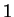 is a positive number.
is a positive number.
To see that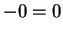 , let's suppose that there is number
, let's suppose that there is number 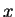 which is the
additive inverse of
which is the
additive inverse of 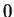 . Then
. Then 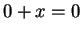 by axiom V.10, and
by axiom V.10, and 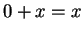 by
axiom V.8 (and V.5). Thus,
by
axiom V.8 (and V.5). Thus, 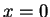 , so
, so 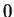 is its own additive inverse.
is its own additive inverse.
Finally, we need the following.Lemma. For all
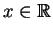 ,
,
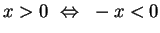 .
.
Proof. Suppose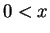 . Then by axiom V.16,
. Then by axiom V.16,
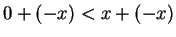 , and
applying axiom V.8 to the right and V.10 to the left, we get
, and
applying axiom V.8 to the right and V.10 to the left, we get 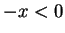 .
.
Similarly, if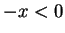 , we have
, we have
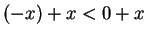 , so
, so 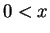 .
.
Whew! More than I bargained for here.
- There are integers
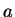 and
and 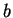 so that
so that 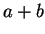 is positive and
is positive and 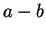 is
negative.
is
negative.
Solution: True. Since we need merely demonstrate existence of such
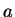 and
and 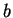 , let
, let
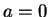 and
and 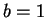 . Then
. Then 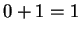 is positive (we just did this), and
is positive (we just did this), and 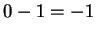 is negative (again, see the previous part.)
is negative (again, see the previous part.)
- For every integer
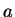 , there is an integer
, there is an integer 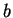 so that
so that 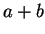 is
positive and
is
positive and 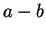 is negative.
is negative.
Solution: This is true. We must show that given a specific integer
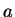 , we can find
an integer
, we can find
an integer 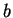 that meets our needs. Let's break the problem up into three
possibilities:
that meets our needs. Let's break the problem up into three
possibilities: 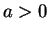 ,
, 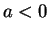 , and
, and 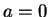 .
.
Case I:
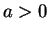 . Let
. Let 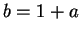 . First, notice that
. First, notice that 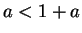 , since
, since 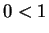 and so by axiom V.16,
and so by axiom V.16, 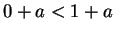 . By transitivity of
. By transitivity of 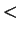 (axiom V.14), we have
(axiom V.14), we have 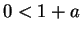 . Thus, again by V.16,
. Thus, again by V.16,
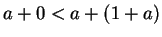 . Thus (by transitivity again)
. Thus (by transitivity again) 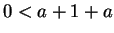 , so
, so 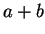 is
positive.
is
positive.
We also need show that
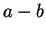 is negative. Note that
is negative. Note that
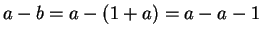 (distributive law, commutivity), and so
(distributive law, commutivity), and so
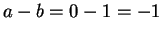 . (using associativity, additive identity). But
. (using associativity, additive identity). But 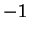 is negative,
from before.
is negative,
from before.
Case II:
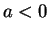 . Now let
. Now let 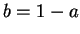 . Then
. Then
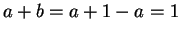 , and
, and 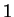 is
positive. To see that
is
positive. To see that 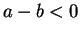 , we have
, we have
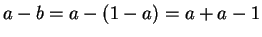 . Using the fact that
. Using the fact that 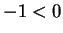 and
and 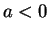 , together with
transitivity and axioms V.14 and V.16, we get
, together with
transitivity and axioms V.14 and V.16, we get 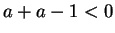 .
.
Case III:
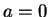 . Easiest of all. Let
. Easiest of all. Let 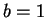 , so
, so 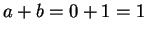 ,
which is positive, and
,
which is positive, and
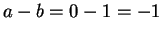 , negative.
, negative.
- There is an integer
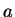 so that, for every integer
so that, for every integer 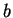 ,
, 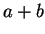 is
positive and
is
positive and 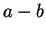 is negative.
is negative.
Solution: This is false. This says that we can find this
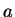 , and write it
down somewhere. Now for this
, and write it
down somewhere. Now for this 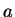 and any possible
and any possible 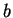 ,
, 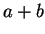 must be
positive and
must be
positive and 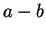 negative. What about the choice
negative. What about the choice 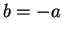 ? It is
supposed to be positive, but
? It is
supposed to be positive, but
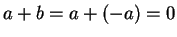 , which isn't positive.
, which isn't positive.
Another way to see this is to write it in symbols. This statement is
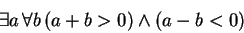
and its negation is
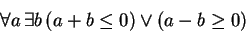
But this follows from the previous part. Since the negation is true, the statement can't be.
- m(x) means ``x is male''.
- f(x) means ``x is female''.
- P(x,y) means ``x is the parent of y''.
- (K1)
-
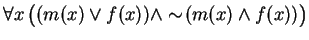
- (K2)
-
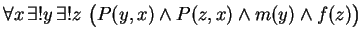
- State carefully, in common English, the meaning of axiom K1.
Solution: Axiom K1 says
For every person, either the person is male or female, but that person cannot be both male and female.
This is better said asEvery person is either male or female, but not both.
- State carefully, in common English, the meaning of axiom K2.
Solution:
For every person
This is a very stilted way to say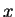 , there is a unique person
, there is a unique person 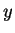 and a unique
person
and a unique
person 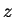 so that
so that 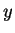 and
and 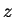 are parents of
are parents of 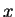 ,
, 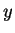 is male, and
is male, and
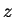 is female.
is female.
Everybody has exactly one father and exactly one mother.
provided that we know that ``father'' means ``male parent'' and ``mother'' means ``female parent''.
- Define the predicate
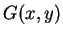 to mean
to mean
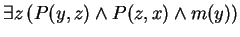 .
What is the common English meaning of
.
What is the common English meaning of 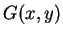 ?
?
Solution:
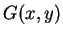 means
means
since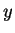 is a grandfather of
is a grandfather of 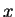
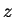 is a parent of
is a parent of 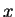 and
and 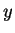 is
is 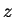 's father.
's father.
- What is the meaning, in common English, of the assertion
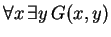 ?
?
Solution:
Everybody has a grandfather.
- Prove that
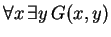 .
.
Solution: Let
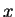 be an arbitrary person. Then by axiom
be an arbitrary person. Then by axiom 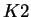 ,
, 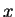 has a father,
that is, there is some
has a father,
that is, there is some 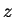 for which
for which 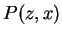 and
and 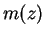 .
Now apply axiom
.
Now apply axiom 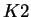 again to this new
again to this new 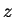 to get
to get 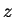 's father, who we
shall denote
's father, who we
shall denote 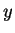 . Since
. Since 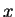 's father's father is his/her grandfather,
we have
's father's father is his/her grandfather,
we have 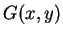 . (Of course, there is also the maternal grandfater).
We have shown that for this
. (Of course, there is also the maternal grandfater).
We have shown that for this 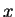 ,
,
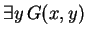 .
Since
.
Since 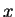 was arbitrary, we apply UG to conclude that
was arbitrary, we apply UG to conclude that
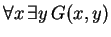 .
.
Solution:
We want to establish that
![]() , where
, where ![]() is
the statement ``
is
the statement ``![]() is divisible by
is divisible by ![]() . Using induction as
suggested, we first check
. Using induction as
suggested, we first check ![]() :
:
Is ![]() divisible by
divisible by ![]() ? Since
? Since ![]() , yes it is.
, yes it is.
Now we show that
![]() , that is, we want to show
, that is, we want to show
![]() is divisible by
is divisible by ![]() if we know that
if we know that ![]() is.
is.
If ![]() is divisible by 3, then there is an
is divisible by 3, then there is an ![]() so that
so that ![]() .
Consequently,
.
Consequently, ![]() . So, we have
. So, we have
We have shown that