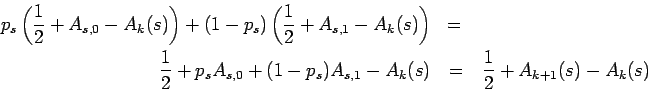Next: Further results on pseudo-random
Up: Pseudo-random number generators
Previous: The Next Bit Theorem
Contents
Subsections
The Efficient Test Theorem
When we are given a sequence of bits from a pseudo-random number generator,
we often test the quality of the generator by doing things like counting
the fraction of 0's, the fraction of subsequences of the form 111, etc.
A test is defined to be an efficiently computable function
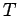 which takes as input a sequence of bits of length
which takes as input a sequence of bits of length 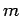 and gives as output a number between 0 and 1. Define
and gives as output a number between 0 and 1. Define
These averages both involve finite operations-- 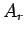 involves adding
up
involves adding
up 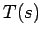 over the
over the 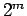 possible
possible 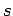 and dividing. Similarly
and dividing. Similarly 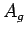 deals with an average over all possible seeds (presumably the number of
possible seeds is much less than
deals with an average over all possible seeds (presumably the number of
possible seeds is much less than 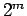 ).
).
It would take too much time to calculate 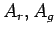 exactly, but they
can be estimated with high probability using the sampling ideas in
section 7.3.
exactly, but they
can be estimated with high probability using the sampling ideas in
section 7.3.
A generator is said to satisfy the test 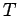 if
if 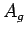 is close
to
is close
to 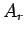 , i. e.,
, i. e., 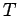 cannot tell the difference between sequences from
the generator and genuinely random sequences. [we are being deliberately
vague about the precise definition of ``close.'']
cannot tell the difference between sequences from
the generator and genuinely random sequences. [we are being deliberately
vague about the precise definition of ``close.'']
Theorem 30
If a generator satisfies the Next Bit Condition, it satisfies all
efficiently computable tests 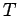 .
.
Proof: We will show that, if we had 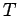 with
with 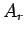 significantly
different from
significantly
different from 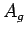 , then for some
, then for some 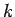 ,
, 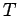 could be used to predict
the
could be used to predict
the 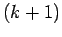 -st bit from the first
-st bit from the first 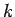 bits with probability somewhat
larger than
bits with probability somewhat
larger than 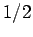 . This would contradict the Next Bit Condition.
. This would contradict the Next Bit Condition.
If 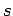 is a sequence of
is a sequence of 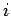 bits, let
bits, let 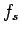 be the fraction of all
possible seeds whose first
be the fraction of all
possible seeds whose first 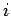 bits are
bits are 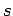 . For some
. For some 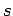 , we may have
, we may have
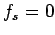 . Note that
. Note that
where the sum is over all 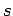 of
length
of
length 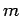 .
.
The proof involves two steps:
- Identify a
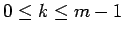 such that the behavior of
such that the behavior of 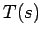 depends in a significant way
on the
depends in a significant way
on the 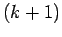 -st bit of
-st bit of 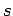 .
.
- Use
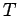 to make a prediction for
the
to make a prediction for
the 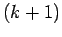 -st bit.
-st bit.
The proof of step 1 uses ideas similar to the ``sampling walk'' used
to prove Theorem 5.1 in the Goldwasser-Micali paper. Define
where the sum is over all 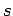 of length
of length
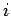 and
and 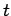 of length
of length 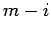 , with
, with 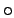 meaning to combine
meaning to combine
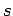 and
and 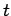 to create a sequence of length
to create a sequence of length 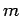 .
.
 is the expected value of
is the expected value of 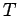 applied to a sequence in which the
first
applied to a sequence in which the
first 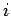 bits come from the generator (using a randomly chosen seed),
with the remaining bits coming from a genuinely random source.
bits come from the generator (using a randomly chosen seed),
with the remaining bits coming from a genuinely random source.
Note that 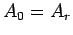 ,
, 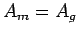 , and that all
, and that all  can be
estimated with high probability using sampling. Since
can be
estimated with high probability using sampling. Since
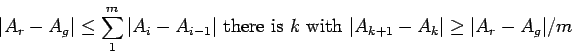 |
(2) |
This completes step 1.14
In step 2, we are concentrating on a specific sequence 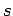 of length
of length
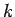 , where
, where 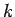 satisfies (2). We
wish to use the behavior of
satisfies (2). We
wish to use the behavior of 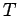 to predict whether the
to predict whether the 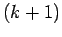 -st bit
should be 0 or 1. Intuitively, we ask
-st bit
should be 0 or 1. Intuitively, we ask 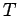 which of the two possibilities
would make the sequence look more random.
which of the two possibilities
would make the sequence look more random.
We will need to look at the analogues of the averages 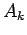 and
and
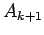 , restricting attention to those sequences which begin with
, restricting attention to those sequences which begin with
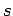 :
:
The definition of 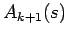 is based on the idea that
is based on the idea that 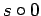 and
and 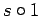 are the only sequences of length
are the only sequences of length 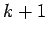 which begin with
which begin with 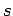 .
Note that, for
.
Note that, for 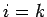 or
or 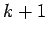 ,
,
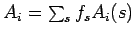 , where the
sum is taken over all
, where the
sum is taken over all 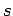 of length
of length 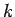 .
.
These are the expected values of 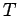 for a sequence which begins with
for a sequence which begins with 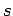 , has
either 0 or 1 as its
, has
either 0 or 1 as its 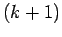 -st term, and continues randomly. They
can be estimated by sampling. Let
-st term, and continues randomly. They
can be estimated by sampling. Let 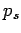 be the
fraction of the seeds which give
be the
fraction of the seeds which give 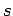 as the first
as the first 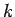 bits which give
0 as the
bits which give
0 as the 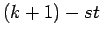 bit (thus
bit (thus
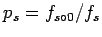 ).
Then
).
Then
If we could estimate 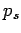 from (4), it would be simple to predict
the next generated bit after
from (4), it would be simple to predict
the next generated bit after 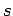 . Unfortunately, we cannot efficiently
estimate
. Unfortunately, we cannot efficiently
estimate 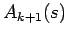 . The problem is that we would have to sample
among the seeds which generate
. The problem is that we would have to sample
among the seeds which generate 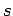 , and there is no easy way to find
such seeds. Instead, we must find a way to use the information that
the average of
, and there is no easy way to find
such seeds. Instead, we must find a way to use the information that
the average of 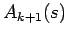 is
is 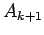 , which we can estimate.
, which we can estimate.
The (far from obvious) idea will be to have the prediction of the
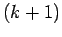 -st bit itself be random. As we will see below, the probabilities
can be assigned to the two possible predictions can be chosen so that
the expected number of correct guesses looks like the right-hand side
of (4).
-st bit itself be random. As we will see below, the probabilities
can be assigned to the two possible predictions can be chosen so that
the expected number of correct guesses looks like the right-hand side
of (4).
We will assume 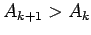 [remember, we chose
[remember, we chose 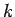 so that the
difference between the two is significant]. The other case can be
handled similarly. If
so that the
difference between the two is significant]. The other case can be
handled similarly. If
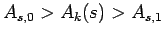 , we would
expect sequences beginning with
, we would
expect sequences beginning with 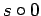 to look more like things
from the generator than sequences beginning with
to look more like things
from the generator than sequences beginning with 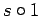 . Our
prediction for the next bit following
. Our
prediction for the next bit following 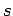 will be random, given by
will be random, given by
[The probabilities add to 1 by equation (3).]
The probability that the prediction for input 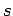 is correct is
is correct is
When we average over all seeds resulting in all possible 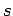 , we get
a correct prediction with probability
, we get
a correct prediction with probability
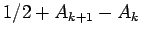 , which,
by (2), is significantly greater than
, which,
by (2), is significantly greater than 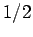 .
15
The Next Bit Condition was stated in a way that clearly distinguished
the beginning of the pseudo-random sequence from the end. By contrast,
the Efficient Test Theorem treats a pseudo-random sequence in a completely
symmetrical way. From that point of view, it does not matter which
end of the sequence is used to start the construction. This leads to
.
15
The Next Bit Condition was stated in a way that clearly distinguished
the beginning of the pseudo-random sequence from the end. By contrast,
the Efficient Test Theorem treats a pseudo-random sequence in a completely
symmetrical way. From that point of view, it does not matter which
end of the sequence is used to start the construction. This leads to
Corollary 31
Let 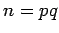 . Start with a random
. Start with a random 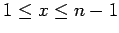 not divisible
by
not divisible
by  or
or 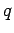 . Let
. Let 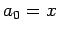 ,
,
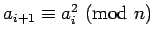 . The sequence of
bits given by
. The sequence of
bits given by 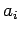 mod 2 satisfies all efficient tests.
mod 2 satisfies all efficient tests.
Footnotes
- ... 1.14
- Instead of estimating
all the
 , we could begin by estimating
, we could begin by estimating 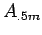 . We would next
estimate either
. We would next
estimate either 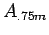 or
or  , depending on whether
, depending on whether 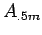 was closer to
was closer to 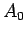 or
or 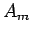 .
.
- ....
15
- Thanks to R. Sengupta for pointing out the importance of the
expression for
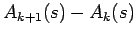 .
.




Next: Further results on pseudo-random
Up: Pseudo-random number generators
Previous: The Next Bit Theorem
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() which takes as input a sequence of bits of length
which takes as input a sequence of bits of length ![]() and gives as output a number between 0 and 1. Define
and gives as output a number between 0 and 1. Define
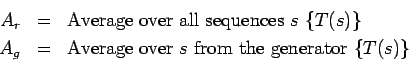
![]() exactly, but they
can be estimated with high probability using the sampling ideas in
section 7.3.
exactly, but they
can be estimated with high probability using the sampling ideas in
section 7.3.
![]() if
if ![]() is close
to
is close
to ![]() , i. e.,
, i. e., ![]() cannot tell the difference between sequences from
the generator and genuinely random sequences. [we are being deliberately
vague about the precise definition of ``close.'']
cannot tell the difference between sequences from
the generator and genuinely random sequences. [we are being deliberately
vague about the precise definition of ``close.'']
![]() is a sequence of
is a sequence of ![]() bits, let
bits, let ![]() be the fraction of all
possible seeds whose first
be the fraction of all
possible seeds whose first ![]() bits are
bits are ![]() . For some
. For some ![]() , we may have
, we may have
![]() . Note that
. Note that
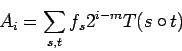
![]() ,
, ![]() , and that all
, and that all ![]() can be
estimated with high probability using sampling. Since
can be
estimated with high probability using sampling. Since
![]() of length
of length
![]() , where
, where ![]() satisfies (2). We
wish to use the behavior of
satisfies (2). We
wish to use the behavior of ![]() to predict whether the
to predict whether the ![]() -st bit
should be 0 or 1. Intuitively, we ask
-st bit
should be 0 or 1. Intuitively, we ask ![]() which of the two possibilities
would make the sequence look more random.
which of the two possibilities
would make the sequence look more random.
![]() and
and
![]() , restricting attention to those sequences which begin with
, restricting attention to those sequences which begin with
![]() :
: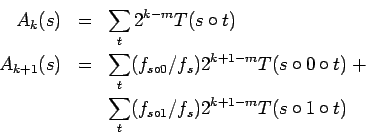
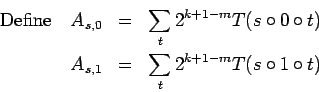
![]() -st bit itself be random. As we will see below, the probabilities
can be assigned to the two possible predictions can be chosen so that
the expected number of correct guesses looks like the right-hand side
of (4).
-st bit itself be random. As we will see below, the probabilities
can be assigned to the two possible predictions can be chosen so that
the expected number of correct guesses looks like the right-hand side
of (4).
![]() [remember, we chose
[remember, we chose ![]() so that the
difference between the two is significant]. The other case can be
handled similarly. If
so that the
difference between the two is significant]. The other case can be
handled similarly. If
![]() , we would
expect sequences beginning with
, we would
expect sequences beginning with ![]() to look more like things
from the generator than sequences beginning with
to look more like things
from the generator than sequences beginning with ![]() . Our
prediction for the next bit following
. Our
prediction for the next bit following ![]() will be random, given by
will be random, given by
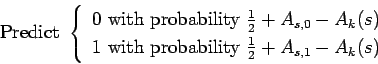
![]() is correct is
is correct is