Turtle Graphics

Imagine you have a small turtle who responds to certain commands like ``move forward a step'', ``move back a step'', ``turn right'', and ``turn left''. Imagine also that this turtle carries a pen (or just leaves a trail of green slime wherever he crawls-- the pond he came out of was none too clean). As long as our turtle follows our commands without tiring, we can get him to make rather intricate patterns easily.^5.1The turtle graphics commands described here are not a standard part of maple. Rather, they are in a file ``turtle.txt'' which we will examine in more detail later in this chapter. Maple has a somewhat different implementation included in the share library. In order to get our turtle commands known to maple, we must first load them with a command such as

> read(`turtle.txt`);

Let us suppose our turtle is given a string such as ``FLFRF'' and interprets it as the sequence of instructions ``Move Forward. Turn Left. Move Forward. Turn Right. Move Forward.'' Then we should see the turtle move in a zigzag pattern:

> TurtleCmd(`FLFRF`);

We shall begin assuming the turtle knows the following commands:

F -- move forward one step		R -- turn right (but don't move)
B -- move backward one step		L -- turn left

We will point out some more commands later, although this set is sufficient to do quite a lot.^5.2 For example, we can ask our turtle to make a self portrait:

> 
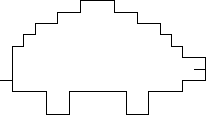
  TurtleCmd(`FRFLFFF RFFLFFLFFR FFFFF RFFLFFLFFR FFFLFR FFLF RBFL 
             FLFF RFLFRFLFRFLF FRFLFFRFLFFF LFRFFLF RFFLF RFLFRFLF FFF`); 

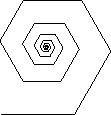
Or, we can make a spiral:

> 
  TurtleCmd(`FRFR FFRFFR FFFFRFFFFR FFFFFFFFRFFFFFFFR`);

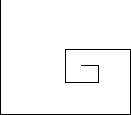
This last can be represented more succinctly if we add a pair of new commands, namely

G -- ``Grow'', i.e. double the unit of length      S -- ``Shrink'' (halve the unit of length)

Then the last picture can be produced by the string ``FRFRG FRFRG FRFRG FRFR'', or, even better, we can make it spiral much more by repeating ``FRFRG'' twenty times:

> 
  TurtleCmd(cat(seq(`FRFRG`,i=1..20)));

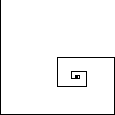
You may have noticed that the command TurtleCmd always resizes the resulting graphic to be of constant width. While this may seem a minor point, it is not. In any single string of turtle commands, ``FF'' will always be twice as long as ``F''; however, TurtleCmd(`F`) and TurtleCmd(`FFFFFFFFFF`) produce identical results. This is because the a single ``F'' in the second case is 1/10 the width of the figure, while it is the full width in the first case.

We can also adjust some of the turtle's attributes. For example, the turtle need not make only 90 degree turns. We use the command ResetTurtle() to set the turtle back to its initial state, then SetTurtleAngle to specify the angle (in degrees) that the turtle will turn left or right when it encounters an L or R command.

> 
  ResetTurtle(); SetTurtleAngle(60);
  TurtleCmd(cat(seq(`FRFRG`,i=1..20)));

Here is a somewhat prettier example. Can you figure out what is happening?

> 
  ResetTurtle(); SetTurtleAngle(30);
  TurtleCmd(cat(seq(cat(`L`,
                        seq(`FL`,i=1..12)),
                    j=1..12)));

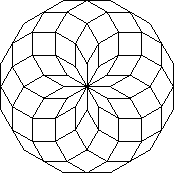
SetTurtleScale allows us to modify the behavior of the S and G commands. Its argument is the factor the unit of length changes when an S is encountered.

> 
  ResetTurtle(); SetTurtleAngle(60); SetTurtleScale(.8);
  TurtleCmd(cat(seq(`FRFRG`,i=1..20)));

Footnotes

... easily.^5.1

This is the premise of the computer language LOGO, invented in the late 1960s and often used to teach children the basic ideas of programming. The ``turtle graphics'' we do here has very little to do with real LOGO, which is a much more powerful system.

... lot.^5.2

In fact, this set of commands is already redundant. We could replace L with RRR and B with RRFLL.