


Next: The Sierpinski gasket
Up: A turtle in a
Previous: Fractal Dimension
The set 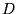 of the previous section is an example of a Cantor
set. Often, a Cantor set is described as the result of an iterative
process, much in the same way we described the Koch curve in
§2. We'll describe the most common Cantor set,
the ``middle-thirds Cantor set'', this way now.
of the previous section is an example of a Cantor
set. Often, a Cantor set is described as the result of an iterative
process, much in the same way we described the Koch curve in
§2. We'll describe the most common Cantor set,
the ``middle-thirds Cantor set'', this way now.
Begin with the interval [0, 1] as the set  .
Now remove the open interval
(
.
Now remove the open interval
(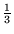 ,
,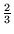 ) from
) from
 to obtain
to obtain
To get the second stage, we remove the middle third of each
interval in 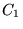 . This gives
We continue in this way, removing the middle third of each interval in
. This gives
We continue in this way, removing the middle third of each interval in
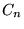 to obtain
to obtain
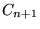 (See Fig. 3).
Note that
(See Fig. 3).
Note that
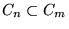 for all n > m. What is left as we let
n
for all n > m. What is left as we let
n 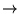
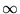 is the Cantor set. That is,
is the Cantor set. That is,
Figure:
The first few stages
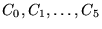 in
the construction of the middle-thirds Cantor set
in
the construction of the middle-thirds Cantor set 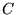 .
.
 |
It may not be clear at first that 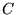 even exists. It seems we
are taking just about everything out when we remove the intervals.
Indeed, the total length of intervals we remove is
even exists. It seems we
are taking just about everything out when we remove the intervals.
Indeed, the total length of intervals we remove is
That is, the total length of the segments removed is equal to the segment we
started with! For this reason, a set like 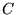 is sometimes called a
``Cantor dust''. But notice that the endpoints of each interval of
is sometimes called a
``Cantor dust''. But notice that the endpoints of each interval of
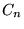 must be in
must be in 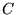 , because they never get removed at any
level. Thus,
, because they never get removed at any
level. Thus, 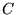 is nonempty, since it contains at least the points
is nonempty, since it contains at least the points
 0, 1,
0, 1,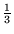 ,
,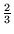 ,
,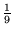 ,
,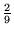 ,
,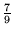 ,
,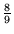 ,
,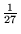 ,
,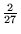 ,.... And
it contains quite a few more points, as well.
To see that, we can view
,.... And
it contains quite a few more points, as well.
To see that, we can view 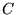 in a manner similar to the
description of the set
in a manner similar to the
description of the set 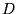 given in
§5.2. However,
given in
§5.2. However, 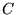 is more naturally
described in base 3, rather than base 10. Let's briefly review what
we mean by this.
is more naturally
described in base 3, rather than base 10. Let's briefly review what
we mean by this.
When we express a number x in base 10, we are expressing it as sums of
powers of ten. Thus, when we write
e5 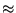 148.413, we are actually saying that
148.413, we are actually saying that
e5 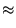
1
. 10
2 + 4
. 10
1 + 8
. 10
0 + 4
. 10
-1 + 1
. 10
-2 + 3
. 10
-3.
There is nothing magic about powers of 10, of course (except that it
is the base we learned as children, and the base used by just about
every living human5.14for everyday numbers). For example, we could express this5.15in ternary (that is, base 3), where we would have
e5 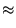
12111.102011
3 = 1
. 3
4 + 2
. 3
3 + 1
. 3
2 + 1
. 3
1 + 1
. 3
0 + 1
. 3
-1 + 0
. 3
-2 + 2
. 3
-3 + 0
. 3
-4 + 1
. 3
-5 + 1
. 3
-6.
In computer applications, the bases 16 (hexadecimal) and 2 (binary)
are very common, because the computer represents everything internally
in binary.5.16
Returning to the Cantor set 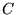 , note that when we remove the
interval
(1/3, 2/3), we are removing all the numbers whose ternary
expansion has a 1 immediately after the decimal place.5.17At the next stage, we remove those points which have a 1 in the
second place after the decimal, and so on. Thus, in the limit, we
obtain the following alternate description of
, note that when we remove the
interval
(1/3, 2/3), we are removing all the numbers whose ternary
expansion has a 1 immediately after the decimal place.5.17At the next stage, we remove those points which have a 1 in the
second place after the decimal, and so on. Thus, in the limit, we
obtain the following alternate description of 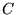 :
:
You may remember that rational numbers correspond to numbers with a
decimal expansion that eventually repeats; the same holds true of the
expansion in any base (how might you prove this if you assume it for
decimals?). It is easy to see using this description that 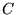 is closed (that is, it contains all its limit points), totally
disconnected, and contains an uncountable number of elements (there
are a lot of sequences of 0s and 2s), just like the set
is closed (that is, it contains all its limit points), totally
disconnected, and contains an uncountable number of elements (there
are a lot of sequences of 0s and 2s), just like the set
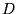 of the previous section. It is also self-similar, because
if we take any small section of it and expand it by an appropriate
power of 3, it looks like the entire set.
of the previous section. It is also self-similar, because
if we take any small section of it and expand it by an appropriate
power of 3, it looks like the entire set.
What is its box dimension? The description by the sets 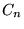 give us an effective way to calculate the limit: at the
nth stage, we have 2n intervals of length 3-n.
Using this, we can immediately calculate that
give us an effective way to calculate the limit: at the
nth stage, we have 2n intervals of length 3-n.
Using this, we can immediately calculate that
You may have noticed the strong similarity in the construction of the
Koch curve 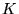 of §2 and the middle-thirds
Cantor set
of §2 and the middle-thirds
Cantor set 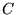 . In fact, notice that the intersection of
. In fact, notice that the intersection of
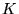 with its base (the initial segment
with its base (the initial segment 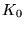 ) is exactly
the middle-thirds Cantor set.
) is exactly
the middle-thirds Cantor set.
Footnotes
- ... human5.14
- Some Native American peoples used base 20,
and the Babylonians were very fond of base 12 and base 60 (consider
how we measure time).
- ... this5.15
- Maple will convert integers to other bases, using a command such as
convert(148, base, 3). One has to work a little bit to convert
fractions-- can you think of a way to do this?
- ... binary.5.16
- Hexadecimal is convenient for use with a binary system, because we can
group blocks of 4 binary digits to obtain one hexadecimal digit (by
convention, the letters A-F are used to represent the integers 10-15).
This is quite handy in computer applications, because a single byte is
represented by 8 binary digits (bits), or two hex digits. Before 8-bit bytes
became standard, octal (base 8) was very common as well. Octal is much
less convenient for 8-bit quantities, however, because 8 bits don't
break up nicely into groups of 3 bits.
- ... place.5.17
- As in decimal expansions, some points have two
representations. Thus, the point 1/3 can be written either
as .13 or as
.0222
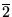 .... As in the construction
of
.... As in the construction
of 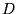 in §5.2, we keep such points in
our set.
in §5.2, we keep such points in
our set.



Next: The Sierpinski gasket
Up: A turtle in a
Previous: Fractal Dimension
Translated from LaTeX by Scott Sutherland
2002-08-29
![]() of the previous section is an example of a Cantor
set. Often, a Cantor set is described as the result of an iterative
process, much in the same way we described the Koch curve in
§2. We'll describe the most common Cantor set,
the ``middle-thirds Cantor set'', this way now.
of the previous section is an example of a Cantor
set. Often, a Cantor set is described as the result of an iterative
process, much in the same way we described the Koch curve in
§2. We'll describe the most common Cantor set,
the ``middle-thirds Cantor set'', this way now.
![]() .
Now remove the open interval
(
.
Now remove the open interval
(![]() ,
,![]() ) from
) from
![]() to obtain
to obtain
![$\displaystyle \Cal{C}_1 = \set{ \left[0,\frac{1}{3}\right], \left[\frac{2}{3}, 1\right]}.$](img620.gif)
![$\displaystyle \Cal{C}_2 =
\set{ \left[0,\frac{1}{9}\right], \left[\frac{2}{9...
...ght],
\left[\frac{2}{3}, \frac{7}{9}\right], \left[\frac{8}{9}, 1\right]}.$](img622.gif)
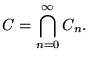
![]() even exists. It seems we
are taking just about everything out when we remove the intervals.
Indeed, the total length of intervals we remove is
even exists. It seems we
are taking just about everything out when we remove the intervals.
Indeed, the total length of intervals we remove is
![]() 148.413, we are actually saying that
148.413, we are actually saying that
![]() , note that when we remove the
interval
(1/3, 2/3), we are removing all the numbers whose ternary
expansion has a 1 immediately after the decimal place.5.17At the next stage, we remove those points which have a 1 in the
second place after the decimal, and so on. Thus, in the limit, we
obtain the following alternate description of
, note that when we remove the
interval
(1/3, 2/3), we are removing all the numbers whose ternary
expansion has a 1 immediately after the decimal place.5.17At the next stage, we remove those points which have a 1 in the
second place after the decimal, and so on. Thus, in the limit, we
obtain the following alternate description of ![]() :
:
![]() give us an effective way to calculate the limit: at the
nth stage, we have 2n intervals of length 3-n.
Using this, we can immediately calculate that
give us an effective way to calculate the limit: at the
nth stage, we have 2n intervals of length 3-n.
Using this, we can immediately calculate that
![]() of §2 and the middle-thirds
Cantor set
of §2 and the middle-thirds
Cantor set ![]() . In fact, notice that the intersection of
. In fact, notice that the intersection of
![]() with its base (the initial segment
with its base (the initial segment ![]() ) is exactly
the middle-thirds Cantor set.
) is exactly
the middle-thirds Cantor set.