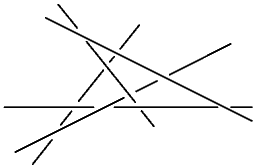Configurations of Skew Lines in the 3D Space
by Julia Viro and Oleg Viro
This is about links made of lines. One has to require that the lines are not only disjoint, but also non-parallel. This gives the lines an ability to be linked with each other. As long as the number of lines is not large (less than 6), the linking numbers rule. Then the Jones polynomial comes. On a horizont the Khovanov homology can be recognized...

Pictorial Calculus for Isometries,
American Mathematical Monthly 123, January 2016

Introductions into Topology of Real Algebraic Varieties

Introductions to patchworking
Gluing of spaces is a landmark of topology. Cut and paste techniques like surgery, Dehn surgery, connected sum, decomposition along incompressible surfaces are usual there.
In Algebraic Geometry more rigid and rich structure makes spaces reluctant to allow such a rude treatment. However, sometimes an algebraic variety can be described topologically using cut and paste operations borrowed from topology. Pathworking is a technique providing varieties made of patches.

Dequantization of real algebraic geometry on logarithmic paper
A talk by Oleg Viro at the Third European Congress of Mathematicians (Barcelona, 2000). It bridged patchworking and Litvinov - Maslov dequantization of positive real numbers and started up a broad development of Tropical geometry.

What is an Amoeba?   Notices AMS, 49:8 (2002), 916-917, [pdf]
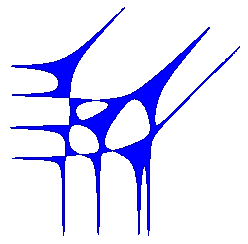In mathematical terminology the word amoeba is a recent addition introduced in 1994. A mathematical amoeba falls short in being similar to its biological prototype. In the simplest case, it is a region the plane, which may pretend to be a picture of amoeba: a body with several holes (vacuoles) and straight narrowing tentacles (pseudopods) reaching to infinity. A planar amoeba is the image of the zero locus of a polynomial in two variables under the map $$(\mathbb C\smallsetminus0)^2\to\mathbb R^2: (z,w)\mapsto(\log|z|,\log|w|)$$

On Euler's footsteps, Evgeny Shchepin's Uppsala lectures on Calculus. During the Fall Semester of 2001 Prof. Evgeny Shchepin (Moscow Steklov Institute) gave lectures on Calculus for an advanced group of first year undergraduate students at Uppsala University. The course followed the historical development of Analysis: it started with series, but limits appeared only in the middle, after integrals. Complex analysis appeared on an early stage motivated by the needs of real analysis. All turns of the course are internally motivated.
Each lecture contains something surprising. For instance, in the first lecture it is proved that the sum of all the non-negative integer powers of two (i.e., 1+2+4+8+16+32+...) equals -1, and a practical interpretation of this equality is presented.

Elementary Topology. Textbook in Problems,
by O.Ya.Viro, O.A.Ivanov, V.M.Kharlamov and N.Y.Netsvetaev.