Visualizing Women in Science, Mathematics and Engineering
  • Home
  • Posters
  • Materials for Study
  • Biographies
  • Cool Links
  • The Design Team


    • Visualizing Mathematics

    Is it possible to "see" four dimensions?

    Here's an exercise which may illuminate some of the mystery.

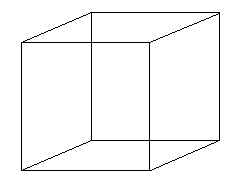
    Look at the cube. First off, notice that while a cube is a three-dimensional object, your flat computer screen is only two-dimensional. In other words, we are able to represent three-dimensional objects using only two dimensions. This should give you some hope that we can get an insight into the fourth dimension.

    Now, back to the cube. How many cubes can you see in the above graphic?

    I can see two . Maybe it would help if I colored them in:

    Now, back to the original drawing:

    Can you see the two cubes, both hiding there in the one picture? Here's the fun part. Look at the picture and focus on one of the cubes, it doesn't matter which one. Now, slowly, in your mind, shift your focus to the other cube. There is a moment when the lines have to "jump" through one another. Do you see it? The shift you are doing is an example of a fourth-dimensional shift.

    You can find out more about dimension on the Squeezing the Phase Space page.

    Let's move on. You don't have to go to four dimensions to experience weird and wacky objects. Here are two exercises for you to try:

    • Can you imagine a two-dimensional surface which only has one side?
    • Can you imagine a one-dimensional figure which has an infinite perimeter, but bounds a finite area?

    Play around with these ideas, and see if you can come up with some interesting shapes. When you're done you can read about some famous examples:

    One thing we can learn from these examples is that our geometric intuition -- what we think we know just from looking at pictures -- can be misleading. The following is a classic example.

    Which of the following two line segments is longer?

    Of course, it is also true that we can learn a lot from pictures. The following exercise shows just how much information pictures can convey, and how our minds are able to work at visual pattern recognition.

    In each of the following groups of four pictures, decide which is the odd one out.

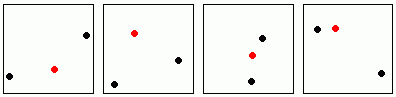
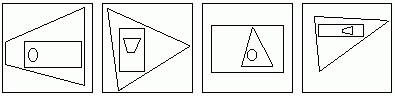
    Here are my solutions. Using mine as examples, see if you can come up with puzzles of your own. Can you design one that your friends can't work out (but which they think is clever when you tell them the answer?)