Squeezing the Phase Space

What do we mean when we say that we live in a three-dimensional space? This is a question worth thinking about. Many of you will suggest that objects in our space have three ``dimensions,'' namely length, width and height. This answer is on the right track, but it is important to separate the two meanings of dimension, the one that means ``size,'' and the one that is intended when we say space is 3-dimensional. A precise mathematical definition exists, but a good rough idea comes from noticing that it takes three numbers to locate a point (in this room, for example). Starting from the door, go 6 feet forward, then 2 feet to the right and take the point 4 and a half feet above the floor. These instructions locate a unique point in the room, and every point in the room can be specified by a suitable combination of three numbers. Similarly the position of an airplane can be completely described by giving a longitude, a latitude and a height above the ground.

What would a 2-dimensional space be like? What would it be like to live in a 2-dimensional space? Think about it. This question was brilliantly and amusingly answered by Edwin A. Abbott, a British schoolmaster who lived from 1838 to 1926. He wrote a book called `` Flatland, A Romance of Many Dimensions.'' The book is about life in a 2-dimensional world. As the title suggests, a 2-dimensional space is flat, like the surface of the blackboard, or like the floor in this room. We can use our earlier understanding of dimension here too: it takes two numbers to locate a point on the blackboard; likewise on the Earth's surface, which is flat in this sense, any point can be located by its longitude and latitude.

Cultural note: ``Flatland, A Romance of Many Dimensions'' tells the story of life and the relations between the sexes in a 2-dimensional world inhabited by polygons. It is easy to misread the story as sexist, but in fact Abbott was lampooning the social and educational insitutions of his day. ``The place, Flatland, was a sexist society, but the book "Flatland" is intended, and was received, as social satire and more. Its author was ... a leader in the movement to bring educational opportunities to young women in Victorian England, '' according to Thomas Banchoff, the leading American Abbott scholar. For more information on this point, see Social Satire in Flatland in the Math Forum (Math Awareness Month 2000). For a deeper treatment of Abbott's life and work, see Banchoff's From Flatland to Hypergraphics: Interacting with Higher Dimensions.

How about a 1-dimensional space? The simplest is a line, or part of a line. There a point can be located by exactly one coordinate. An example of a 0-dimensional space is a single point. In that space there is nowhere to go, and it takes no numbers to tell where you are.

Geometric shapes in dimensions 1, 2, 3.

Geometric shapes are the simplest objects that can exist in space. In our 0-dimensional space the only object is the point itself. The simplest 1-dimensional geometric shape is a line segment: let us make it of length one to be specific. In dimension 2 we have various choices. What are they? Let us pick one example, a one-by-one square. Similarly for a simple 3-dimensional object we pick a one-by-one-by-one cube. Look at the lineup:

point
line segment of length one
one-by-one square
one-by-one-by-one cube.

Can you see any relations between them? After you think a while, maybe you will have noticed that

the cube has six faces, and each is a one-by-one square;
the square has four sides, and each is a segment of length one;
the segment has two ends, and each is a point;
we can complete this by saying that the point has no edges at all.

Here is another relation you may have seen:

if you move a point a distance of one unit, it draws a segment of length one;
if you move the segment a distance of one unit (perpendicularly to itself), it draws a one-by-one square;
if you move the square a distance of one unit (perpendicularly to itself), it draws a one-by-one-by-one cube.

Can you find any other patterns like these?

Perspective.

In art, perspective means the technique of drawing three-dimensional things on a two-dimensional sheet of paper. Suppose we want to draw our 3-dimensional cube on a 2-dimensional sheet, or on the 2-dimensional blackboard. What does the picture look like? Try it. Do you all get the same picture?

The picture most people get looks like this:

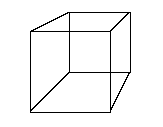
But suppose your eye was just outside one face of the cube. Then you would see this:

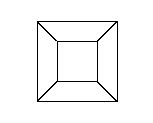
(For more mature students) How far would your eye have to be from the face for the back face to seem half as wide as the front?

On to 4 dimensions: the hypercube.

The list of simple geometric shapes does not have to stop with the cube! We can talk about a 4-dimensional shape that would be a one-by-one-by-one-by-one hypercube. Suppose we tried to extend the two patterns of relations. What would we get? Try to extrapolate the patterns yourselves. You will probably guess:

the hypercube has eight ``faces'' and each is a cube.
if you move the cube a distance of one unit (perpendicularly to itself), it draws a one-by-one-by-one-by-one hypercube.

Exactly! But how can we move a cube ``perpendicularly to itself?'' We can't, of course, not in three-dimensional space. This maneuver can only be carried out in a 4-dimensional space. Does that mean it is impossible? Not mathematically! After all, when we talk about ``moving the square a distance of one unit perpendicularly to itself'' we don't actually have to physically move it, we can just imagine moving it. In the same way we can imagine moving the cube a distance of one unit through a fourth dimension. In ``Flatland,'' Abbott makes us think about how hard it is for the two-dimensional Flatlanders to imagine a third dimension. But just as they can imagine three dimensions without being able to ``see'' them, we can imagine four.

Just as we can draw a 2-dimensional perspective picture of a 3-dimensional cube, we can build a 3-dimensional perspective model of a 4-dimensional hypercube. We will use the perspective in which our eye is one unit away from a ``face'' of the hypercube, so the back ``face'' seems half as wide as the front. Then the perspective model will look like this:

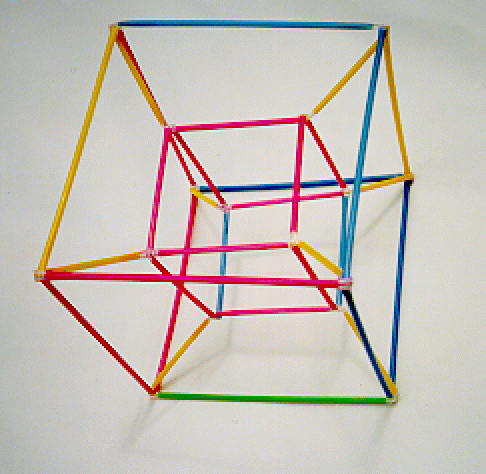
A 3-dimensional perspective model of the hypercube.
Can you find the eight 3-dimensional cubical faces?
Use the 2-dimensional perspective picture of the cube to give
you a hint -- what happens to the six square faces of the cube?

Building a model of the hypercube.

The model is made of drinking straws. They are joined by connectors, each of which is an `X'-shape made of two 2-inch lengths of straw stapled together at their centers.

Making the connectors: use a small stapler, like a baby Tot Swingline. Position the stapler so that one tine of the staple goes through the center of the top straw. The model requires 16 connectors.

The outside three-dimensional cube is made of 12 full-length straws joined with connectors.

Inserting the connectors: fold one of the four ends of the connector so it has a `U'-shaped cross-secton. Then you can slide it into the end of the straw. When you let go, it will expand and grip.

The inside three-dimensional cube is made of 12 half-length straws joined with connectors.

The assembly seems to work better if the connectors on the outside cube are arranged to that the outward-pointing connector ends come from the outer of the two straw-segments that make up the connector; and oppositely for the inside cube.

The two cubes are joined corner to corner by eight linking straws. (More mature students) How long should the linking straws be? For practical assembly they should be made somewhat shorter than the ideal length.

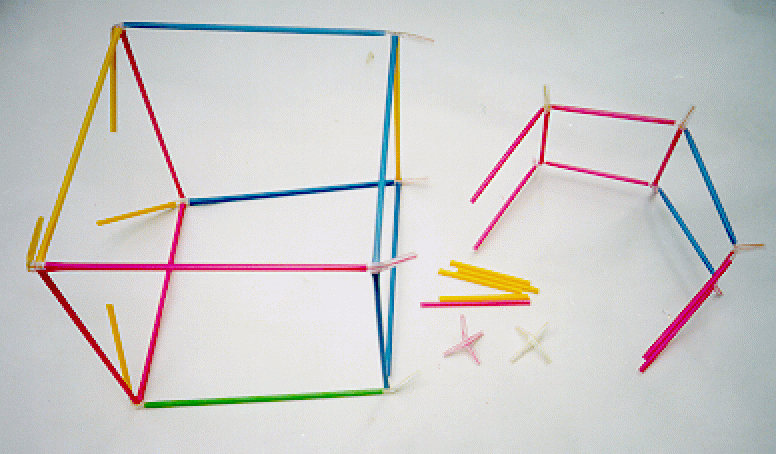A partly assembled hypercube model. Note the two unattached connectors
and the relative length of the red half-straw and the yellow linking straws.

Topics for Further Thought.

1. Can you push the patterns further and describe a 5-dimensional cube, a 6-dimensional cube, ... ?

2. How many vertices do the point, segment, square, cube, hypercube have? Can you figure out how many vertices an n-dimensional cube would have? Hint: one of the patterns of relations will help you.

3. The Euler characteristic (pronounced ``oiler'') of a geometric shape is (number of vertices) - (number of edges) + (number of 2-dimensional faces) - (number of 3-dimensional faces) + ... alternating plus and minus up to the dimension of the shape, where there is always one top-dimensional ``face,'' the shape itself. Check that for the point, segment, square, cube and hypercube the Euler characteristic is exactly 1. Hard problem: prove this for the n-dimensional cube.

4. Another simple 2-dimensional shape is the equilateral triangle of side-length one. The corresponding 3-dimensional shape is the tetrahedron of side-length one. This gives a new family: point, segment, triangle, tetrahedron,... . Notice that the triangle can be constructed from the segment by choosing a point not on the line of the segment, and joining it to each point of the segment. Then the point can be positioned to make all the new edges of unit length. Check that the segment can be constructed from the point in this way, and the tetrahedron from the triangle. The hypertetrahedron is the next member of the family. Let us call the point the 0-simplex, the segment the 1-simplex, the triangle the 2-simplex and the tetrahedron the 3-simplex, so the hypertetrahedron is the 4-simplex. Find the analogue, for the family of simplexes, of the first pattern of relations in the family of cubes.

5. Build a 3-dimensional perspective model of a hypertetrahedron. Work by analogy with what you did with cube and hypercube. What is the analogous 2-dimensional perspective drawing of a tetrahedron? Calculate the lengths of the new elements in the perspective model (hard); otherwise fit them by trial and error.

6. Check, for n = 0, 1, 2, 3 and p < = n that the number of p-dimensional faces of the n-simplex is equal to the binomial coefficient C(n+1,p+1). Hard problem: prove this for a general n and p < = n.

7. Prove that the Euler characteristic of the n-simplex is 1.