
The seeds in this pine-cone lie on two sets of spirals: 13 right-handed ones numbered in blue, 8 left-handed ones numbered in red.
The most striking aspect of phyllotaxis, certainly from a mathematical point of view, is the appearance of Fibonacci numbers. Since their definition is purely computational, their ubiquity in nature immediately poses two questions. Why do these particular pairs of numbers appear? How are these patterns generated? Sir D'Arcy Wentworth Thompson, the father of mathematical morphology, understood that these question have no biological meaning:
| "... while the Fibonacci series stares us in the face in the fir-cone, it does so for mathematical reasons; and its supposed usefulness, and the hypothesis of its introduction into plant-structure through natural selection, are matters which deserve no place in the plain study of botanical phenomena" [5]. |
The first purely mathematical attack on the problem seems to have been in the 1907 book "Mathematical and microscopic-anatomical studies of Phyllotaxis ..." [6](in German) by the Dutch mathematical biologist Gerrit van Iterson. He studied what he called "regular arrays of circles on a cylindrical surface." These are packings of identical circular discs around a cylinder so that each is tangent to four nearest neighbors, with no overlapping, and so that their centers are at the vertices of a linear lattice on the cylinder. (The discs were bent to conform to the bending of the cylinder).
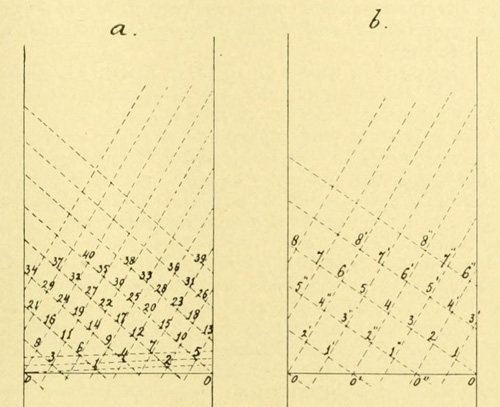
Figure 1 from [6]. It shows two linear lattices on a cylinder. Here the cylinder has been slit along a generator and unrolled in the plane: a lattice becomes two non-parallel sets of regularly spaced lines; their intersections are the lattice points. Lattice a is "simple" because a single "principal spiral" runs through all the lattice points; for lattice b three spirals would be necessary.
Van Iterson considers simple lattices, and among simple lattices those which give the densest packing. These will occur when the two sets of parallel lines have the same spacing, and intersect at a 120o angle.
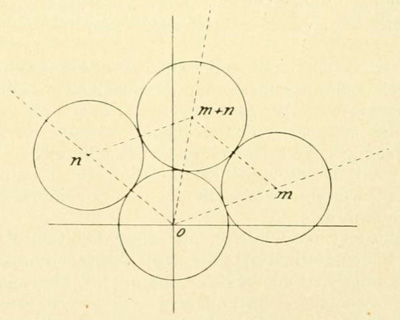
Van Iterson's Figure 11. Neighboring discs in a regular array. Following numbers along the principal spiral, discm is the first to touch disc0; discn is the second. Regularity forces discm+n to be tangent to both discm and discn. Dense packing will occur when, as shown here, discm+n is also tangent to disc0. In that case van Iterson speaks of "three-numbered" contact. Each disc will lie on three "contact spirals," with slopes m, n and m+n.
Finally, van Iterson investigates what happens when the diameter a of the circle is varied with respect to the circumference A of the cylinder. The three simplest cases are m = 0, n = 1 (when a = A), then m = 1, n = 1, and m = 1, n = 2.
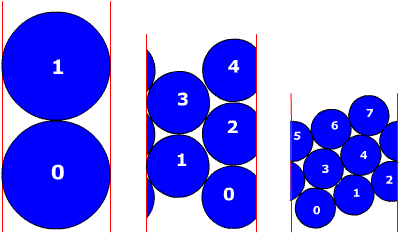
The three simplest dense circle tilings I, II, III correspond to the pairs (0, 0), (1, 1) and (1, 2). Notice that III occurs in two mirror-image forms.
If we think of the transition from one packing to the next as driven by compression, then we can understand the move from II to III as circle 3 slipping between 1 and 2 to touch 0 (it can do this in two different directions). If we want to compress one of the forms of III we can slide 4 down between 1 and 3 to touch 0, giving (1, 3), or we can slide 5 down between 2 and 3 to touch 0, giving (2, 3). Generally, van Iterson showed that the (m, n) tiling (m < n) can compress to (m, m+n) or (n, m+n). This means that the pairs (m, n) that can occur in dense disk tilings of a cylinder correspond to the Farey numbers m/n: this is the listing of the rational numbers between 0 and 1 by layers: layer (-1) contains 0/1 and 1/1; layer 0 contains 1/2; and in general layer k contains all "Farey sums" of nearest-neighbor rationals in the union of the lower-numbered layers; the Farey sum of p/q and r/s is the rational (p+r)/(q+s). One can check that the (m, n) thus obtained are always relatively prime.
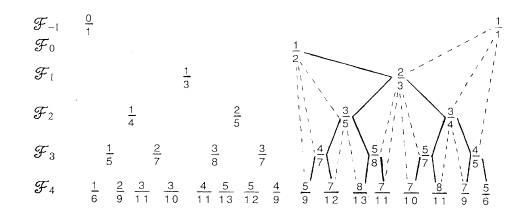
The first few layers of the Farey numbers. Each entry is the Farey sum of the two above it. The solid lines join a number to its "younger" parent (this will be significant later). Figure from [2]: L. S. Levitov, Phyllotaxis of Flux Lattices in Layered Superconductors, Phys. Rev. Lett. 66 224, © APS, used with permission.
The study of phyllotactic phenomena in physics started in 1991 with theoretical work [2] of L. S. Levitov on arrays of vortices in layered superconductors. He showed there that as the analogue of a compression parameter increased, the vortices would assemble in arrays described by Farey numbers of higher and higher levels. But as he demonstrated later that year [3] for a large class of point-point repulsion potentials (see also [1]), the bifurcations, after the first one, are not symmetrical: the physics privileges the fork going in the direction opposite from that of the previous one. It follows that in most cases the morphology of an array will fall along the sequence (1, 2), (2, 3), (3, 5), (5, 8), ... corresponding to quotients of successive Fibonacci numbers. If the switch at 2/3 is missed, then the sequence will run (2, 3), (3, 4), (5, 7), (8, 11), ... (later forks are even more energetically biased). This is the explanation for the occurrence of the two sequences in physical phenomena, and presumably also for their occurrence in nature: one also encounters the alternate phyllotaxis 2, 3, 4, 7, 11, ... , although much less often than the standard one; other arrangements are extremely rare.
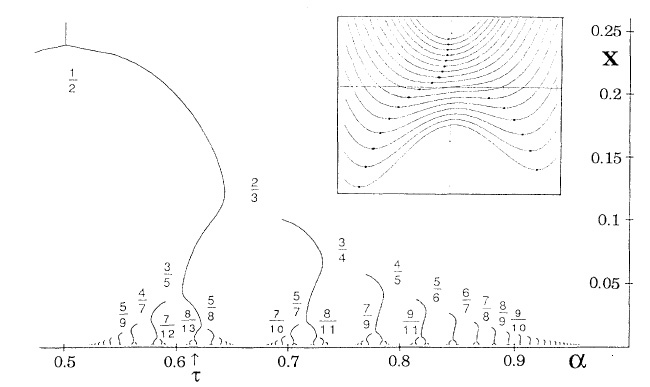
From [2] as above, used with permission. This diagram shows the theoretical history of the vortex array configurations as the "compression" parameter (inversely related to X) is increased. Forking towards the older children is energetically disfavored (the inset shows a configuration parameter tracking the potential minimum near a "pseudo-bifurcation"). The Farey numbers that occur converge to τ = (√5 -1)/2 = .618033... in the limit. (τ and its inverse 1/τ = τ + 1 share the name "the golden mean").
The magnetic cactus (illustrated below) is an experimental device constructed by Cristiano Nisoli, Nathaniel Gabor, Paul Lammert, J. D. Maynard and Vincent Crespi [4] to investigate phyllotaxis as a purely physical phenomenon.

The magnetic cactus is a vertical stack of 50 rings, each 2.2cm in diameter, mounted on ball bearings along a 40cm-long aluminum rod. Each ring bears an iron-neodymium magnet mounted radially with the South pole pointing out; so nearby magnets repel each other. The equilibrium angle ω (Ω below) between nearest-neighbor rings is the main parameter in this study. Image courtesy of Cristiano Nisoli.
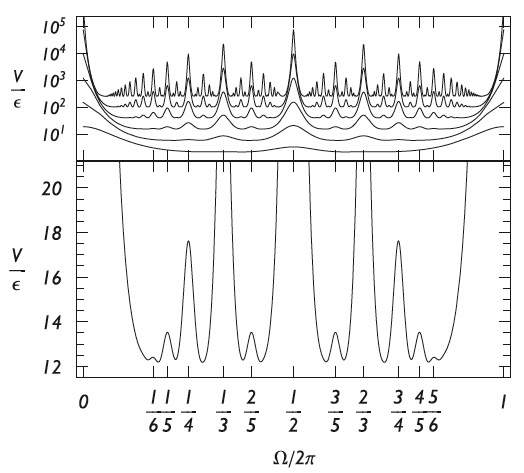
(above) The potential energy of a magnetic cactus of radius R
with magnets vertically a
units apart and adjacent magnets uniformly separated by an angle
Ω, plotted against Ω for (from the bottom) six successively halved values of a/R, starting with a/R = 0.5.
(below) The same for the a/R = 0.15 of the experiment. Image courtesy of Cristiano Nisoli.
Here are the results of their experiment, run with the a/R = 0.15 of their apparatus:
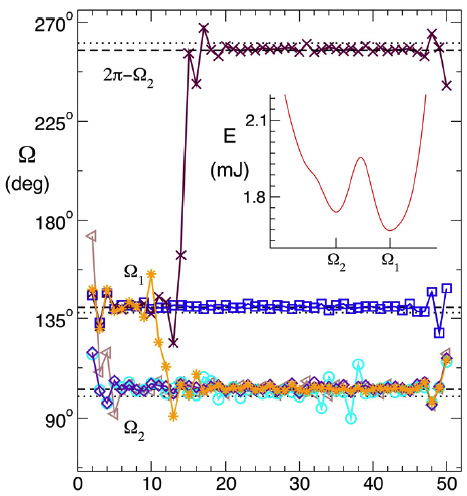
The angular offset between successive magnets in the cactus, measured as more and more magnets are added to the stack. The angles converge rapidly to one of the "phyllotactic angles" Ω1, Ω2 and 2π-Ω2. The first is 2π(1 - τ) = 137.5o, the "golden angle." (Note that 2πτ, which strangely does not appear, would be equally golden in the opposite direction). The second, Ω2 = 99.5o and its complement 2π-Ω2 = 260.5o occur when the system goes towards 3/4 on the second bifurcation, and then tracks through 5/7, 8/11, ... to an alternate limit. Image courtesy of Cristiano Nisoli.
Nisoli and his team use their physical apparatus to investigate the dynamics of such a system. They report several new and very interesting phenomena, unfortunately beyond the scope of this column. Please see [4] for more details.