This month's topics:

• "Samurai mathematician"
• The diagonalization of physics
• Science goes to MathFest
• Math meets the campaign ad on YouTube

Seki Takakazu (Seki Kowa). Image from Tensai no Eiko to Zasetsu by Masahiko Fujiwara (Shincho-sha, Tokyo, 2002), used with permission.

"Samurai Mathematician Set Japan Ablaze With Brief, Bright Light" is the title of a History of Science NewsFocus piece in the October 10 2008 Science. Dennis Normile reports from Tokyo, site of a history of mathematics conference last August dedicated to the memory of Seki Takakazu. Seki (c. 1642-1708, also Seki Kowa) was in fact born into a samurai family; his portrait includes the the two swords (daisho) attesting his warrior status. That he "set Japan ablaze" may be an overstatement, but the "bright light" is appropriate: Seki (an almost exact contemporary of Leibniz, but working in complete isolation from European mathematics) "devised new notation for handling equations with several variables and developed solutions for equations with an unknown raised to the fifth power." Furthermore, according to Normile, "His most significant work focused on determinants ... , a field he pioneered a year or two ahead of ... Leibniz." The word "brief" is, unfortunately, also correct. Seki was ahead of his time, and soon after his death, even though his works were gathered and preserved by his students, "the Japanese mathematical tradition hit a dead end." Normile quotes the science historian Hikosaburo Komatsu: Seki's more erudite work "was too difficult for people to pick up and carry forward." Only now are his most innovative contributions being recognized. Namely, his "discovery around the year 1680 of a general theory of elimination, a method of solving simultaneous equations by whittling down the number of unknown quantities one by one." According to Komatsu, the work had been overlooked because it led to calculations "almost beyond human capabilities."

Cantor's diagonal argument occurs in his (second, 1891) proof of the uncountability of the real numbers. As Wikipedia tells us, "it demonstrates a powerful and general technique, which has since been reused many times in a wide range of proofs, also known as diagonal arguments ... The most famous examples are perhaps Russell's paradox, the first of Gödel's incompleteness theorems, and Turing's answer to the [Halting Problem]." Now this technique has been extended to the real world, or at least to our understanding of it. Philippe Binder reports in a Philosophy of Science News & Views piece in Nature (October 16, 2008) on work of the physicist/generalist David Wolpert published earlier this year (Physica D 237 1257-1281). According to Binder, Wolpert has demonstrated "that the entire physical Universe cannot be fully understood by any single inference system that exists within it." How does he get there? In Binder's telling, Wolpert "introduces the idea of inference machines -- physical devices that may or may not involve human input -- that can measure data and perform computations, and that model how we come to understand and predict nature." These machines process U, "the space of all world-lines (sequences of events) in the Universe that are consistent with the laws of physics." Wolpert defines strong inference as "the ability of one machine to predict the total conclusion function of another machine for all possible set-ups." And then he uses diagonalization to prove:

1. "Let C₁ be any strong inference machine for U. There is another machine, C₂, that cannot be strongly inferred by C₁.
2. No two strong inference machines can be strongly inferred from each other."

MathFest 2008 was held from July 31 to August 2 in Madison, Wisconsin. Barry Cipra was on hand and reported on items of general interest in the September 5 2008 issue of Science. Among his selections:

• Circle packings on tori. William Dickinson (Grand Valley State University, Allendale, Michigan) and a team of undergraduates have spent two summers exploring the question. These are flat tori, coming from the identification of opposite sides in a parallelogram. The problem varies with the geometry of the parallelogram. Last summer, two of the students (Daniel Guillot and Anna Castellaz) found the densest packing for 5 equal circles on the "triangular" torus (= two equilateral triangles):
  

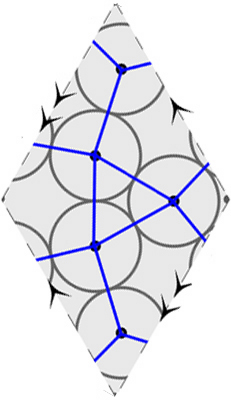
  The densest arrangement of 5 equal circles on the triangular torus covers 71.1% of the area. Images courtesy of William Dickinson.

  Another student (Sandi Xhumari) solved the problem for 6 circles this summer. "Together, the ideas they developed enabled Dickinson to nail down the densest packing for five circles on the square torus."
  

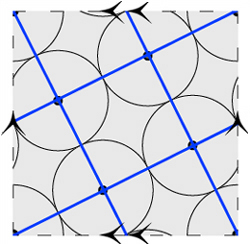
  On the square torus, the densest packing of 5 equal circles covers π/4 = 78.5% of the area.

• Hinged dissections.
  

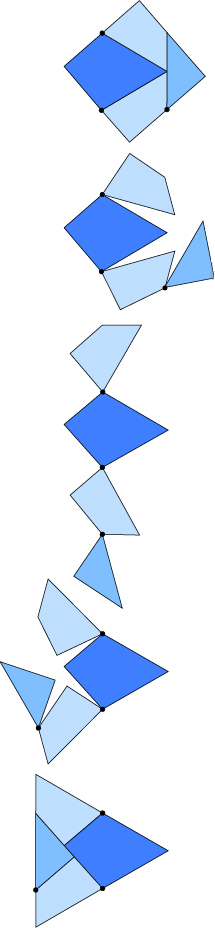  "In the early 19th century, mathematicians proved that any two polygons with the same area can be cut into a finite number of matching pieces. For example, it's possible to cut a square into four pieces and rearrange them into an equilateral triangle." For the square and triangle, it was shown by Henry Dudeney in 1902 how to hinge the pieces together so that the pieces could swing from one configuration to the other. His dissection is shown on the left: the four pieces rotate on their hinges (black dots) to reassemble the square into a triangle, and vice-versa. Image courtesy Erik Demaine. Recently Demaine (MIT) and collaborators have shown that any polygonal dissection can be turned into one with hinges, and have extended the work into three dimensions. Cipra: "In 3D, unfortunately, equal volume doesn't guarantee the existence of a dissection. But when dissections do exist, the MIT group's construction shows that they can be refined into hinged dissections." The work is written up here.

Click to watch. "The Thinking Man," created by R. Larkin Clarke. This may amuse or infuriate you, but it does seem to involve some kind of mathematics. Thanks to Jonathan Farley for the timely link.