Topology and Elementary Electric Circuit Theory, II: Duality

Note. After the first part of this series was posted, I learned that electric circuit theory from a topological viewpoint had been briefly treated in Applications of Algebraic Topology by the great topologist Solomon Lefschetz (Springer-Verlag, New York-Heidelberg-Berlin, 1975). I am grateful to Graham Norton for this information.

Introduction

For our purposes an electrical circuit will be an oriented planar graph in which each edge bears an electrical element: a voltage source, a current source, a resistor, a capacitor or an inductor.

Geometric duality

An planar graph $G$ has a geometric dual graph $g$. This notion requires the outside of the graph to be considered a face (which is natural when the graph is drawn on a spherical surface).

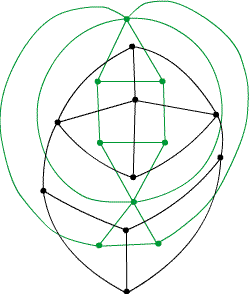
Construction of the (green) geometric dual to a (black) graph. There is a green vertex in the center of each black face; two are joined by a green edge if the black faces have an edge in common.

Here $G$ is the graph drawn in black; the geometric dual will be green. Put a green vertex inside each face of $G$, including the "outside" face. This vertex will be the dual of that face. Next if two of the faces of $G$ shage a (black) edge, draw a green edge between the two green vertices, which intersects the black edge in exactly one point. These two edges are dual. This gives all the edges of the geometric dual graph, and the faces they enclose (including an "outside" one) are the faces of the dual. Notice that the dual of a black $k$-valent vertex (i.e. one with $k$ incident edges) is a green $k$-gon; dually, the green vertex inside a black $j$-gon will have valence $j$.
Geometric duality is a reciprocal relation: the same procedure, starting with the green graph, will yield the black one.

Oriented duality

Some essential elements of an electric circuit have a direction: a voltage source has a positive terminal and a negative one; a current source generates current flowing in a certain direction. So the graph underlying an electric circuit most be oriented. Before defining a dual circuit we need to define the dual of an oriented graph.

Suppose the black graph is oriented, in the sense that a direction has been picked along each black edge. Here is an algorithm —I learned it from Ernst Guillemin's Introductory Circuit Theory (Wiley, New York, 1953)— for orienting the green graph. Starting from the geometric dual, associate clockwise orientation of an edge of the boundary of a black face with the dual edge pointing outward from the dual vertex. This gives a green oriented graph. Next take a mirror-image reflection of that graph. This is the dual oriented graph. When this algorithm is applied to the dual oriented graph, it gives back the black oriented graph we started with.

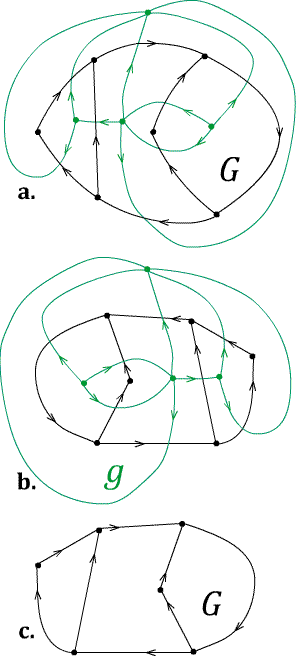
Illustration of the dual oriented graph algorithm and its reciprocity. a. Start with the oriented graph $G$ (black). Construct its geometric dual as above and orient its edges outward from a vertex if the dual edge is oriented clockwise in the dual face, inward otherwise. b. The mirror image of the oriented geometric dual is the (green) dual oriented graph $g$. To show reciprocity, construct the geometric dual of $g$ and orient its edges as above. c. The mirror image of that graph is the original oriented graph $G$.

Electrical duality 1: Voltages, currents, resistors

Since the circuits we are considering are oriented planar graphs, a circuit has a dual oriented graph. It is slightly more mysterious that to each device on an edge (voltage source, current source, resistor, capacitor or inductor) corresponds a dual device on the dual edge giving a dual circuit which can look quite different but which has an isomorphic solution when voltages and currents are interchanged.

We will start with circuits containing only voltage sources, current sources, and resistors. Capacitors and inductors, which respond to changes in currents and voltages, will be introduced later.

Device Duality
$X$ volt voltage source	$X$ ampere current source
$X$ ampere current source	$X$ volt voltage source
$X$ ohm resistor	$1/X$ ohm ($X$ mho) resistor

A circuit $C$ has an undelying oriented graph $G_C$. We construct the dual circuit $c$ on the dual oriented graph: the edge dual to the edge $e_j$ of $G_C$ gets the device dual to the device on $e_j$, following the table above, respecting orientations.
Circuit duality principle: the equation solving for the current in an edge of $C$ is identical to the equation solving for the voltage in its dual edge $c$, and vice-versa.
Here is the simplest non-trivial example.

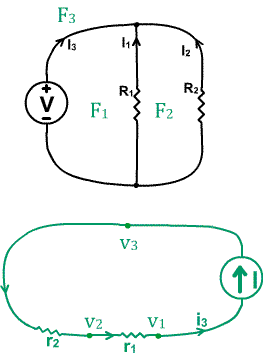
A voltage-resistor circuit $C$ (black) and its dual circuit $c$ (green), constructed as above. (The mirror-reversal is not significant at this stage, but is included for congruence with the treatment of reciprocity above).

We solve for the current $I_3$ in $C$ and for the voltage $v_3-v_1$ along its dual edge in $c$, using Kirchhoff's laws and Ohm's law as described in part 1 of this series.

Solving for $I_3$. Since $V=-R_1I_1$ and $V=-R_2I_2$, it follows that $I_1=-V/R_1$, $I_2=-V/R_2$ and $$I_3= -I_1-I_2 = \frac{V}{R_1} + \frac{V}{R_2} = V(\frac{1}{R_1}+\frac{1}{R_2}).$$
Solving for $v_3-v_1$. $$v_3-v_1= (r_1+r_2)I = I(\frac{1}{R_1}+\frac{1}{R_2}).$$

Since the numbers $V$ and $I$ are the same, as per the table above, the solutions are identical.

Electrical duality 2: adding in Inductors and Capacitors

Inductors and capacitors are time-dependent devices; to study them we use variable voltage and current sources $V(t)$ and $I(t)$; all the currents and voltages in the circuit will now be functions of time. Ohm's law and its analogues for inductors and capacitors read as follows.

resistor
R ohms $V_b(t)-V_a(t) = RI(t)$

inductor
$L$ henrys ${\displaystyle V_b(t)-V_a(t) = L\frac{dI(t)}{dt}}$

capacitor
$C$ farads ${\displaystyle V_b(t)-V_a(t) = \frac{1}{C}\int_{t_0}^tI(t)~dt}$

The rules for constructing a dual circuit now include:

Device Duality

$X$ henry inductor $X$ farad capacitor

$X$ farad capacitor $X$ henry inductor

The simplest example of the duality principle now comes from these two dual circuits. (Adapted from lecture notes published at the School of Electrical Engineering & Computer Science, KAIST, Daijon, Korea.)

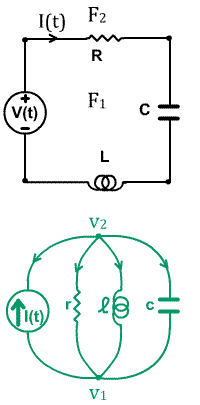
RLCduals

We solve for $I(t)$ in the top circuit and for $(v_2-v_1)(t)$ in the dual.

Use Kirkhhoff's voltage law:
${\displaystyle -V(t)+RI(t)+\frac{1}{C}\int_{t_0}^t I(s)~ds + L\frac{dI(t)}{dt}=0}$
differentiating gives
${\displaystyle L\frac{d^2I(t)}{dt^2}+R\frac{dI(t)}{dt} +\frac{1}{C}I(t) = \frac{dV(t)}{dt}}.$
Use Kirkhoff's current law:
${\displaystyle -I(t)+\frac{1}{r}(v_2-v_1)(t)+ \int_{t_0}^t \frac{1}{\ell} (v_2-v_1)(s)~ds + c \frac{d(v_2-v_1)(t)}{dt}=0}$
differentiating gives
${\displaystyle c \frac{d^2(v_2-v_1)(t)}{dt^2}+ \frac{1}{r}\frac{d(v_2-v_1)(t)} {dt} + \frac{1}{\ell} (v_2-v_1)(t) = \frac{dI(t)}{dt} }.$

Since (see table) $c=L$, $\ell = C$, ${\displaystyle\frac{1}{r}=R}$ and $I(t)=V(t)$, the expressions are identical.

Geometric duality in higher dimensions

The idea is very general and extends to geometric structures that are locally like Euclidean $n$-dimensional space. Such a structure has a dual, where to each $k$-dimensional element is associated an element of the complementary dimension $n-k$ (since $1+1=2$, in our graphs the dual of an edge is an edge). For example, in the $4$-dimensional cube pictured here, the dual of the marked edge would be a triangle with one vertex in the blue cube, one in the green cube and one in the pink.

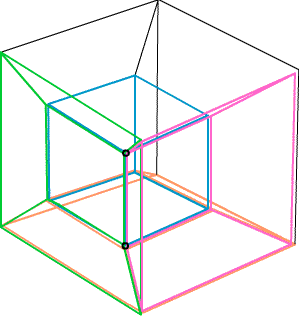
A cube in four dimensions is itself a 3-dimensional polytope. It has eight 3-dimensional cubes as its faces. (In this image, the eighth cube is the outside).

resistor R ohms		$V_b(t)-V_a(t) = RI(t)$
inductor $L$ henrys		${\displaystyle V_b(t)-V_a(t) = L\frac{dI(t)}{dt}}$
capacitor $C$ farads		${\displaystyle V_b(t)-V_a(t) = \frac{1}{C}\int_{t_0}^tI(t)~dt}$

Device Duality
$X$ henry inductor	$X$ farad capacitor
$X$ farad capacitor	$X$ henry inductor