The Early History of Calculus Problems

Introduction

Anyone teaching Calculus has presumably studied Calculus at some point in the past and is probably aware that homework problems assigned today are identical to to the ones we faced as students. How far back can this go? Certainly not beyond 1696, when Guillaume François Antoine, Marquis de L'Hospital (often written L'Hôpital) published Analyse des infiniment petits, pour l'intelligence des lignes courbes, a work known as the very first Calculus textbook; to put that date in perspective: Newton's Principia appeared in 1687. In fact some of today's problems are close, if not identical, to those appearing in this 17th-century text (the Infiniment petits did not have a list of exercises at the end of each section, but L'Hospital illustrates his presentation with many worked-out examples). This column presents five specimens from Section III: "The use of the calculus of differences to find largest and least values."
   L'Hospital's text only covers differential calculus (and, as its title suggests, concentrates on applications to analytic geometry). There is no companion volume on integral calculus; here is the Marquis' explanation: "M. Leibnitz having written me that he was working on the subject in a Treatise which he entitles De Scientiâ infiniti, I did not want to risk depriving the Public of such a beautiful Work which must include all the most intriguing facts about the inverse tangent Method, about rectifications of curves, about quadrature of the spaces they enclose, about those of the surfaces of the bodies they describe, about the dimensions of those bodies, about the location of centers of gravity, &c. I am only making this matter public because he asked me to do so in his Letters ... ." Unfortunately De Scientiâ infiniti, if written, was never published.
   Notation: Much of L'Hospital's notation, derived from Leibnitz, has remained standard, although following Descartes he writes $xx$ instead of $x^2$. The concepts of function and derivative were still in the future. He analyzes a curve from its equation by calculating the relation between the differences $dx$ and $dy$, and locates maxima and minima by looking for points where $dy=0$ (it is understood that $dx\neq 0$).
   Historical note: the text of the Infiniment petits I worked with (a 1768 edition available online, with plates here), once belonged to John Quincy Adams, and bears copious annotations in his hand. It is now in the Boston Public Library.

Example I

Supppose that $x^3+y^3=axy$ (AP $= x$, PM $= y$, AB $= a$) gives the nature of the curve MDM. [Find the point E where the height is largest].

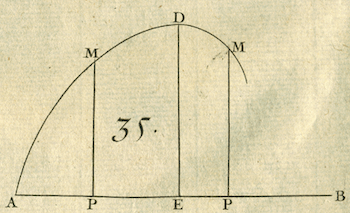
This image and those below appear courtesy of the Boston Public Library.

• Taking differences gives $3xxdx + 3yydy = axdy + aydx$, and $dy = \frac{aydx-3xxdx}{3yy-ax} =0$ when P is the desired point E, from which one derives $y=\frac{3xx}{a}$; and substituting this value for $y$ in the equation $x^3+y^3=axy$, one finds for AE the value $x=\frac{1}{3}a\sqrt[3]{2}$ such that the ordinate ED is greater than all the similarly defined PM. [Today this would be an exercise in "implicit differentiation," a concept that could not have occurred to L'Hospital.]

Example VI

Among all the cones that can be inscribed in a sphere, determine which one has the largest lateral area.

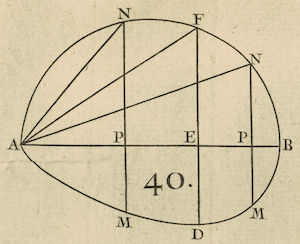
• The question reduces to determining on the diameter AB of the semi-circle AFB the point E; in such a way that having dropped the perpendicular EF, and joined AF, the rectangle AF$\times$FE is the largest of all the similarly defined ones AN$\times$NP. Because if one imagines the semi-circle AFB making an entire revolution about the diameter AB, it is clear that it will describe a sphere, and that the right triangles AEF, APN will describe cones inscribed in that sphere, with the lateral surfaces described by the chords AF, AN in the same proportion as the rectangles AF$\times$FE, AN$\times$NP.
     So set the unknown AE $= x$, and the given AB $= a$; then by the property of the circle AF = $\sqrt{ax}$, EF $= \sqrt{ax-xx}$ and therefore AF$\times$FE $= \sqrt{aaxx-ax^3}$ which should be a maximum. For this one can imagine a curve MDM such that the relation of the ordinate PM $(y)$ to the abscissa AP $(x)$ is expressed by the equation $\frac{\sqrt{aaxx-ax^3}} {a}=y$, and one will seek the point E so that the ordinate ED is larger than all the similarly defined ones PM. One will therefore set the difference $\frac{2axdx-3xxdx}{2\sqrt{aaxx-ax^3}}=0$; from which one derives AE $(x) = \frac{2}{3}a.$
      [This elegant solution is beyond what one could expect from a Freshman; today one asks for the cone of maximum volume, with the hint $V = \frac{1}{3}\pi r^2 h$. The answer turns out to be the same.]

Example VII

It is asked, among all the parallelepipeds equal [in volume] to a given cube $a^3$, and that have for one of their edges a given line $b$, which one has the smallest surface.

• Calling $x$ one of the two sought-for edges, the other will be $\frac{a^3}{bx}$; and taking the faces alternating between the three edges $b, x, \frac{a^3}{bx}$, their sum, i.e. $bx + \frac{a^3}{x} + \frac{a^3}{b}$, will be half of the surface, which should be a minimum . So we consider a curve with equation $\frac{bx}{a}+ \frac{aa}{x} + \frac{aa}{b} = y$, and we find by taking the difference $\frac{bdx}{a}- \frac{aadx}{xx}=0$; from which one derives $xx=\frac{a^3}{b}$, and $x = \sqrt{\frac{a^3}{b}}$; so the three edges of the parallelepiped answering the question will be, the first one $b$, the second $\sqrt{\frac{a^3}{b}}$, and the third $\sqrt{\frac{a^3}{b}}$. Whence we see that the two edges we were seeking are equal to each other.

Example XI

A traveler leaving location C to go to location F must cross two regions separated by the straight line AEB. We suppose that in the region on the side of C, he covers distance $a$ in time $c$, and that on the other, on the side of F, distance $b$ in the same time $c$: we ask through which point E on the line AEB he should pass, so as to take the least possible time to get from C to F.

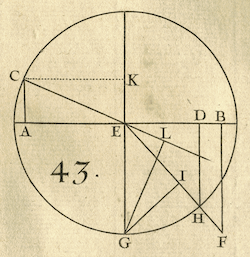
• [L'Hospital gives two analyses leading to the same equation. The first uses geometry; hence the extra constructions in the diagram. The second:] Set AB $= f$, AC $= g$, BF $= h$ and the unknown AE $= x$. Then ... the time the traveler takes to traverse CE is $\frac{c\sqrt{gg+xx}}{a}$ and likewise the time the traveler takes to traverse EF is $\frac{c\sqrt{ff-2fx+xx+hh}}{b}$. This means $\frac{c\sqrt{gg+xx}}{a}+ \frac{c\sqrt{ff-2fx+xx+hh}}{b}$ should be a minimum; and thus the difference $\frac{cxdx}{a\sqrt{gg+xx}}+\frac{bxdx - bfdx}{b\sqrt{ff-2fx+xx+hh}}=0.$ This leads to the equation [As L'Hosptial formats it] $$\begin{array}{ccccc} aax^4 & -2aafx^3 & aaffxx & -2aafggx & +aaffgg = 0\\ -bb &+2bbf & +aagg & & \\ & & -bbff& & \\ & & -bbhh& & \end{array}$$ of which one of the roots will give the sought value for AE.
     [In the Commentaires appended to the 1768 edition, the editor (Aimé-Henri Paulian) remarks: "To find the value of $x$, one will operate on the proposed equation following the rules set down in all elementary algebra texts; we have the right to suppose that one does not read the Infiniment Petits of M. le Marquis de l'Hôpital, without having previously learned to manipulate a fourth order equation." In today's textbooks the problem, usually involving a river, involves walking along one bank and then swimming across; this corresponds to setting $g=0$ in l'Hospital's example, and leads to a quadratic equation.]

Example XII

Let there be a pulley F which hangs freely at the end of a cord CF attached at C, with a plumb bob D suspended by the cord DFB which passes over the pulley F and which is attached at B, in such a way that the points C, B are situated on the same horizontal line. One supposes that the pulley and the cords have no weight; and one asks at what place the plumb bob D, or the pulley F, will rest.

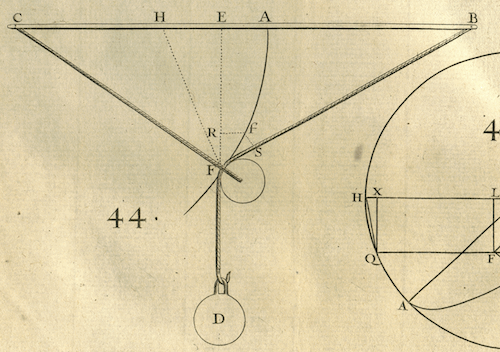
• It is clear from the principles of Mechanics that the plumb bob D will descend as far as possible below the horizontal CB; whence it follows that the plumb-line DFE must be a maximum. Thus calling the givens CF, $a$; DFB, $b$; CB, $c$; and the unknown CE, $x$; one will have EF $=\sqrt{aa-xx}$, FB $=\sqrt{aa+cc-2cx}$, and DFE = $b-\sqrt{aa+cc-2cx}+\sqrt{aa-xx}$ which must be a maximim; and thus the difference $\frac{cdx}{\sqrt{aa+cc-2cx}}- \frac{xdx}{\sqrt{aa-xx}}=0$, whence one derives $2cx^3-2ccxx-aaxx+aacc=0$, and dividing by $x-c$ yields $2cxx-aax-aac=0$, of which one of the roots gives for CE a value such that the perpendicular ED passes through the pulley F and the plumb bob D, when they are at rest. [L'Hospital gives another, geometric, derivation of this equation; hence the extra constructions in the diagram].