Old Babylonian multiplication and reciprocal tables

Introduction

An online survey of Old Babylonian mathematics is available on Duncan Melville's website.

"Old Babylonian" refers here to the civilization that flourished some four thousand years ago (around 2000 B.C.) in what is present-day Iraq. Documents at the time were written in cuneiform ("wedge-shaped") characters on clay tablets, most of them rectangular and of a size to be held comfortably in the hand (about $5\times 8$cm or $2\times 3$ inches). Hundreds of thousands of tablets have been excavated from the ruins of this civilization; perhaps a thousand or so of these concern mathematics. For example, the collection of the University of Pennsylvania Museum of Archaeology and Anthropology, catalogued, with photographs, on the website of the Cuneiform Digital Library Initiative, includes 458 Old Babylonian mathematical tablets (of which about 110 have been published).

For Old Babylonians, mathematics was practical. Many of the mathematical tablets are "problem texts:" they contain problems or sets of problems, sometimes with solutions. Many of the problems involve geometry; the rest are almost always "word problems" where the context is the calculation of the area of an irregular field, the volume of a ditch, the number of bricks to build a ramp, ... . Understanding word problems requires, besides a knowledge of the language used to record them, an thorough understanding of the culture (in particular the different systems of units and their relation). Even the geometry problems require a specialized vocabulary and familiarity with the Babylonian way of explaining a solution. But along with the problem texts are "table texts," which can be understood by anyone who has mastered the Babylonian number system; they are the first known examples of a tradition of mathematical table-making that is still alive and useful today.

Multiplication tables from my Grade 3B notebook. The format is the same as the Old Babylonian (see the 12-times table below). A significant difference is the listing of $0$ as a number; the Old Babylonians had no such symbol.

My thanks to Bill Casselman and to Christian Siebeneicher for furnishing me with images (and to the Yale Balylonian Collection for permission to reproduce NBC 7344); and above all to Jöran Friberg who made me a set of beautiful images of tablets from the Martin Schøyen Collection. References to "Friberg" in this text lead to his book "A Remarkable Collection of Babylonian Mathematical Texts" (Springer, 2007).

The Old Babylonian number system

• Numbers are represented in a base-60 ("sexagesimal") place-value system. This was a local, and very significant, invention; we still retain their notation for the measurement of angles and time: degrees (or hours), minutes and seconds.
• Numbers from 1 to 59 (there is no symbol for zero) are represented by combinations of a symbol for 1 and a symbol for 10. Like Roman numerals using only I and X. The Babylonian numbers from 1 to 20 (plus 30, 40, 50) appear in the central columns of each of the four multiplication tables shown below.
• There is no "decimal point;" as Friberg puts it: "All Babylonian sexagesimal numbers are written as if they were integers, but the intended value of a sexagesimal number in a Babyonian cuneiform text can be its 'nominal' value multiplied by any positive or negative power of 60." The scale of the intended value must be determined by the context.

A ten-times table

In decimal notation a 10-times table is not very interesting, but in base-60 things are less trivial.

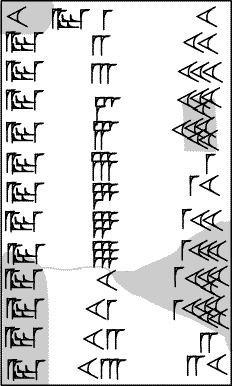
	This 10-times table, tablet VAT7858 in the collection of the Vorderasiatisches Museum, Berlin, exhibits one of the common formats for multiplication tables: the first line (partially illegible here) reads 10 a-rà(times) 1     10. From line 2 on, in this format, the multiplier is left out: a-rà 2     20 a-rà 3     30, stepping up the multiplicand by 1 each time. VAT7858 gives us a nice introduction to Old Babylonian base-60 place-value notation: a-rà 6     1 a-rà 7     1  10 ... a-rà 13     2  10
	The reverse reads a-rà 14     2  20 ... a-rà 19     3   10 a-rà 20     3   20. After 20, as usual, come the multiplicands 30, 40 and 50: a-rà 30     5 and (partially illegible) a-rà 40     6   40 a-rà 50     8   20. The table ends with a colophon, or subscript, usually the scribe's name and the date. Photographs by the late Peter Damerow (Damerow was active in the Cuneiform Digital Library Initiative), courtesy of Christian Siebeneicher.

A five-times table

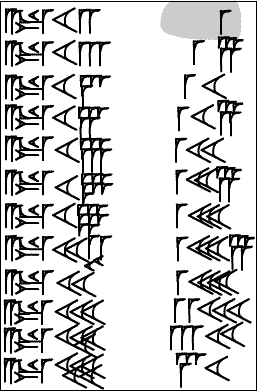
	This 5-times table (tablet NBC7344 in the Yale Babylonian Collection) follows the same format as VAT7858: 5 a-rà 1     5 a-rà 2     10 a-rà 3     15 ... a-rà 11     55.
	The reverse runs from a-rà 12     1 to a-rà 19     1   35 (Note the "subtractive" notation 20 minus 1 for 19, different from the "10+9" of VAT7858) a-rà 20     1   40 a-rà 30     2   30 a-rà 40     3   20 a-rà 50     4   10 . Photographs by Bill Casselman, images used with permission.

A twelve-times table

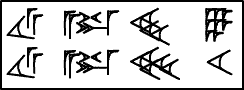
	On this 12-times table (tablet MS2184/3 in the Schøyen collection), the format is different from the more standard NBC7344: the multiplier is repeated on each line: 12 a-rà 1     12 12 a-rà 2     24 ... 12 a-rà 10     2.
	On the reverse: 12 a-rà 11     2   12 ... 12 a-rà 19     3   48 12 a-rà 20     4 12 a-rà 30     6 (the last three lines on the back of the tablet are partially illegible, but note again a special "subtractive" symbol for 19).
	The last two lines wrap around the bottom/top of the tablet: 12 a-rà 40     8   12 a-rà 50     10. Photographs courtesy of Jöran Friberg.

A $1\frac{1}{5}$-times table

	This table (MS3866 in the Schøyen collection) has "head-number" 1 12, so it is a $1\frac{1}{5}$-times table; it follows the standard format: 1 12 a-rà 1     1 12 a-rà 2     2 24 ... a-rà 16     19 12.
	On the reverse the first three lines are partially missing, but they would read: a-rà 17     20   24 a-rà 18     21   36 a-rà 19     22   48 (note another "subtractive" symbol for 19). Then: a-rà 20     24 a-rà 30     36 a-rà 40     48   a-rà 50     1. MS3866 ends with the square of the head-number: 1 12 a-rà 1 12     1 26 24. Photographs courtesy of Jöran Friberg.

A table of reciprocals

The standard Old-Babylonian table gives the reciprocals of the numbers ${\bf \frac{3}{2}}$, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 1, 1 04, 1 21; reciprocals are the sexagesimal numbers with which they multiply to give 1. Some tables omit the ${\bf \frac{3}{2}}$, some also give 1 12, 1 15, 1 20. Since 1 represents any power of $60 = 2^2\cdot 3\cdot 5$, these numbers must all be regular: they can have only 2, 3, and 5 as prime factors.

The numbers in the standard table have the property that they and their reciprocals require no more than three sexagesimal places. If we were to try a similar construction with our decimals, the list could only include $1, 2\leftrightarrow 5, 4\leftrightarrow 25, 8\leftrightarrow 125$ and $16\leftrightarrow 625$.

The tablet shown here is MS3874 in the Schøyen collection. The transcription and (translation) are copied from Friberg.

	1 .da 3" .bi 40 .àm (1, its 2/3, 40 it is); šu.ri.a.bi 30 àm (its half, 30 it is) igi. 3 gál.bi 20: (the opposite of 3 ... is 20) igi. 4 gál.bi 15 igi. 5 gál.bi 12 igi. 6 gál.bi 10 igi. 8 gál.bi 7 30 igi. 9 gál.bi 6 40 igi. 10 gál.bi 6 igi. 12 gál.bi 5 igi. 15 gál.bi 4 igi. 16 gál.bi 3 45 igi. 18 gál.bi 3 20 igi. 20 gál.bi 3 igi. 24 gál.bi 2 30 igi. 25 gál.bi 2 24 igi. 27 gál.bi 2 13 20 igi. 30 gál.bi 2
	The bottom of the tablet is missing. Friberg supplies the rows needed (at the bottom of the obverse and the top of the reverse) to complete the standard table of reciprocals: igi. 32 gál.bi 1 52 30 igi. 36 gál.bi 1 40 igi. 40 gál.bi 1 30 igi. 45 gál.bi 1 20 igi. 48 gál.bi 1 15 igi. 50 gál.bi 1 12 igi. 54 gál.bi 1 06 40 igi. 1 gál.bi 1. The reverse of the table has two legible lines: igi. 1 04 gál.bi 56 15 igi. 1 21 gál.bi 44 26 40. Friberg translates the colophon: this "long tablet" was written by the student ši-ip-suen. Photographs courtesy of Jöran Friberg.

For mathematical coherence, I believe the first two rows should be understood as: "the reciprocal of 3/2 is 40," and "the reciprocal of 2 is 30."