Math in the Media 0603

Math in the Media

June 2003

Math in Nature
Imaginary numbers in The Observer
The Golden Mean in The New York Times
The Poincaré Conjecture (cont.)
Dog bites math

$*$ Math in Nature. The May 15 2003 issue of Nature has at least three articles with interesting mathematical aspects.

Astronomy. "Chaos-assisted capture of irregular moons" is a comparative study of the irregular moon systems of the gas giants Jupiter and Saturn. Irregular moons have highly inclined orbits (but never more than 55 degrees) with respect to the planet's equatorial plane. Their motion may be prograde, counter-clockwise when viewed from above, like our Moon and Jupiter's Gallilean moons, or retrograde. In fact in the Jupiter system, the retrogrades outnumber the progrades 26 to 6. The authors study the 3-dimensional circular restricted three-body problem, focussing on the Sun-Jupiter-moon system. They use a Monte Carlo simulation to show how, in phase space, "the chaotic layer selects for the sense of the angular momentum of incoming and outgoing particles," i.e. sorts them into prograde and retrograde. (Authors: S. A. Astakhov, A. D. Burbanks, S. Wiggins, D. Farrelly)

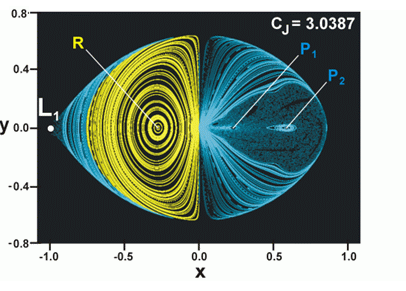
An image from the work of Astakhov et al., showing the Poincaré return map for randomly chosen initial conditions, all at a given energy level E, with motion constrained to the x-y plane. The rectangle represents the central part of the intersection of the hypersurface of energy E in (x,y,px,py) phase space with the hyperplane {px = 0}; only the sheet {dy/dt > 0} is shown. Prograde orbits are blue, retrograde are yellow. R, P₁, P₂ represent periodic orbits. This is one of four images at different energies. Image courtesy David Farrelly.

Econophysics. "A theory of power-law distributions in financial market fluctuations" sets up a model to explain the empirical probabilities:
P(|r_t| > x) ~ x^-3
P(V > x) ~ x^-1.5
P(N > x) ~ x^-3.4 where r_t is the change of the logarithm of stock price in a given time interval Δt (for a given stock), V is trading volume and N is the number of trades. The model "is based on the hypothesis that large movements in stock market activity arise from the trades of large participants." (Authors: X. Gabaix, P. Gopihrishnan, V. Plerou, H. E. Stanley).
Neurophysiology. In "Attractor dynamics of network UP states in the neocortex" the authors report that in analyzing the dynamics of spontaneous activity of neurons in the mouse visual cortex, they detected "synchronized UP state transitions" occurring in "spatially organized ensembles involving small numbers of neurons." (UP is short for the membrane potential depolarized state). They argue that the these synchronized transitions, or 'cortical flashes,' are dynamical attractors, and that "a principal function of the highly recurrent neocortical networks is to generate persistent activity that might represent mental states." (Authors: R. Cossart, D. Aronov, R. Yuste)

$*$ Imaginary numbers in The Observer. The May 18 2003 Observer ran a review of "Imagining Numbers (Particularly the Square Root of Minus Fifteen)" (Allen Lane) by Barry Mazur, the Harvard professor. The reviewer, Jonathan Heawood, leads us past the square root of two ("The geometry is definitive, but the maths goes on for ever") up to the foot of Mt. Imaginary. ("Divorced from the geometric world of shapes and their properties, maths gestures wildly towards a sphere of the unimaginable.") This may not be exactly what Mazur had in mind. Heawood nicely picks up Mazur's metaphor "rather like discovering that there is an efficacious way of getting from Brooklyn to Boston, but that somewhere in mid-journey one has to descend to the Underworld" (for the use of complex numbers in real calculations) as a (unwitting?) paraphrase of G.K. Chesterton's "A merry road, a mazy road, and such as we did tread / The night we went to Birmingham by way of Beachy Head," and ends with the judgment: "I found that I needed more than pencil and paper to make these calculations. I needed a bigger brain. Yet, even without following all his workings-out, the window which Mazur cuts into the world of imaginary numbers is just as exciting, and almost as provocative, as anything in Philip Pullman."

$*$ The Golden Mean in The New York Times. George Johnson contributed an essay to the May 20 2003 Science Times: "Deep in Universe's Software Lurk Beautiful, Mysterious Numbers." The piece begins with a reference to "The Da Vinci Code," a current thriller. "In one of the novel's typically awkward moments" the hero, in full flight from his pursuers, "pauses to reminisce. The subject: a lecture he recently gave at Harvard on the remarkable properties of the number phi." This number (one plus the square root of five, divided by two) is the Golden Mean. Johnson gives the value of φ as 1.6180339; more than Dan Brown, the "Da Vinci" author, who leaves it at 1.618; neither mentions the number's irrationality, which is certainly part of its charm. In the book, φ is connected to goddess-worship via the 5-pointed star "representing the sacred feminine," etc. (The first few Fibonacci numbers also have a role to play). Johnson: "In a world otherwise crippled by math anxiety, books about phi and other so-called constants of the universe are multiplying so quickly that 'The Da Vinci Code' threatens to become part of a genre." He mentions works on φ and Euler's constant γ, taking for granted our familiarity with the recent popularizations of 0, i, π and e, and then veers off into the consideration of numbers in physics. A quick tour of the fine-structure constant, creation theories, counting with stones and the Pythagoreans leads us back to Eugene Wigner and the "phenomenon which might always remain a mystery," The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
Creating a bogus mysterious side to mathematics is certainly not the way to diminish math anxiety. With apologists like these, math needs no enemies.

$*$ The Poincaré Conjecture (cont.) The recent developments were also covered by Science, in an April 18 2003 piece by Dana Mackenzie whose title, "Mathematics World Abuzz Over Possible Poincaré Proof," correctly suggests his Variety-style approach to the subject. "Furthermore, what was to keep the surgeries, like plastic surgeries on a Hollywood star, from going on endlessly?" Nevertheless Mackenzie gives the best layman's guide so far to the history of the problem and to Perelman's innovations. An excellent presentation, ending in a lovely quote from Bennett Chow (UCSD): "It's like climbing a mountain, except in the real world we know how high the mountain is. What Hamilton did was climb incredibly high, far beyond what anyone expected. Perelman started where Hamilton left off and got even higher yet - but we still don't know how high the mountain is."
Nature came back to the story, after last month's "News in Brief" item, with a more elaborate, and mathematically substantial, report by Ian Stewart (May 8, 2003). This account, also excellent, is complementary to Mackenzie's: they emphasize different aspects of the problem and of the putative solution.

$*$ Dog bites math. Lee Dye's May 29 2003 science/technology column for ABCNEWS.com is entitled "Good Dog - Mathematician Explains How His Dog Understands Calculus." Dye is picking up an article in the May 2003 College Mathematics Journal written by Tim Pennings (Hope College, Holland, Michigan). Pennings apparently had been teaching the standard calculus max-min problem that starts "So Tarzan is in the quicksand, and Jane is across the river and down the bank a ways, and she's got to get to him as quickly as possible" in its most modern incarnation. He was out on the shore of Lake Michigan tossing a tennis ball in the water for his Corgi ("Elvis") to retrieve, when he noticed that the dog would run part way down the beach and then cut diagonally out to the ball; just like Jane on her optimal way to rescue Tarzan. Apple : Newton :: Corgi : Pennings. Could it be calculus? Pennings, the story goes, clocked the dog on land and in the water, measured the xs and the ys for various tosses of the ball and plotted the points on a graph. As he told Dye, "it turns out that all the choices he made were right in line, or very close, to the optimal choice." Now Elvis is "on sort of a canine lecture tour, helping Pennings explain calculus to students of all ages." The moral of the story, as Pennings tells it: "Advanced math does have practical applications. If you end up as an industrialist ... and you manufacture a certain item, you will need to come up with a formula that will tell you how many you need to manufacture to maximize your profit, or minimize your cost. And as Elvis would say, if he could speak English, that's calculus." Column available online.

-Tony Phillips
Stony Brook

Math in the Media Archive