Math in the Media
Highlights of math news from science literature and the current media
Math in the Media
Highlights of math news from science literature and the current media
June 2001
Computing an Organism. The e-mail journal Science-Week for May 25 2001 picked
up an item from the March 27 PNAS (98:3879): Stan Marée and
Paulien Hogeweg, of the University of Utrecht, published an account
of their simulation of the culmination behavior of the
social amoeba (``slime mould'') Dictyostelium dicsoideum.
``Computing an organism'' is the title of the accompanying commentary
by Lee A. Segal.
As the
Science-Week editors note, ``The D. discoideum morphogenesis cycle is one of
the great puzzles of biology.'' Briefly, the ``normal'' stage of
this organism is an amoeba, an independent unicellular organism.
It eats bacteria and reproduces by binary fission.
But when a population of these creatures is starving, they aggregate
to form a slug 2 to 4 mm long which moves (``migration'') as a single organism
towards light. There (``culmination'')
the slug puts up a stalk approximately 1 cm
high bearing at its tip a fruiting body containing spores, which eventually
disperse over a wide area, each becoming a new ``normal'' amoeba. Marée
and Hogeweg were able to construct a mathematical model of part of this
amazing behavior, and to use it to run computer simulations of the
process. Their model is a ``a two-dimensional simulation using a hybrid
stochastic cellular automata/partial differential equation schema'' in
which ``individual cells are modeled as a group of connected
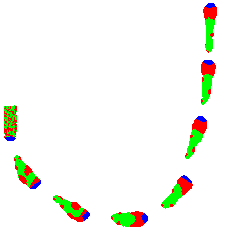
automata: the basic scale of the model is subcellular.'' Here are two
sample printouts. On the left is a simulation of the phototactic
migration, from an earlier work
with their colleague Alexander Panfilov (Proc. R. Soc.
Lond. B (1999) 266, 1351-1360); on the right is a
simulation of the culmination behavior.
|
|
The Science-Week editors conclude: ``...viewing the simulation produced by the mathematical model of Maree and Hogeweg will no doubt startle many biologists. Perhaps the most important consideration is that this work provides evidence that computer modeling involving recognized subcellular dynamic entities may soon be used to predict (and explain) specific tissue development and tissue morphology. The implications for both basic and medical biology are profound.''
Proof on NPR. On April 20, 2001 the National
Public Radio's Online News Hour aired Terence Smith interviewing David
Auburn, author of the Pulitzer-prizewinning play Proof, ``a
family drama that unfolds against the backdrop of mathematical theory.''
Smith asked: ``Did you feel any special burden to explain or make
accessible the world of the mathematician to the audience?''
Auburn's answer: ``The real trick of writing the play was figuring out how
much math to put in it. This ended up being constrained by the story. Since
there is a mystery as to who wrote the mathematical proof, I sort of had to
withdraw information when I could so that I didn't give away the solution to
the mystery but I did try to get in as much lore about the
mathematical profession as I could. In that I was helped a lot by reading
popular books and spending time with mathematicians. We even had some
come in to meet with the cast and talk to them. So that was really
the fun part of doing the play: getting as much of the world of
mathematics into the play as possible and putting it up on stage.''
The segment (which can be read and heard online) includes an excerpt from
the New York performance (HAL was KATHERINE's father's graduate student):
|
HAL: Some friends of mine are in this band - they're playing at a bar up on
Diversity, way down the bill, they probably go on around 2, 2:30, I said I would be there. KATHERINE: Great. HAL: They're all in the math department. They're really great. They have this good song, you'd like it, it's called "I." Lower case I. They just stand there and don't play anything for three minutes. KATHERINE: Imaginary number. HAL: Math joke. You can see why they are way down the bill (laughter). KATHERINE: A long drive to see some nerds in a band. HAL: God, I hate it when when people say that. It's not that long a drive. KATHERINE: So they are nerds. HAL: They are raging geeks but they are geeks that, you know, can dress themselves (laughter) -- hold down a job at a major university. Some of them have switched from glasses to contacts. Play sports. They play in a band. In that sense they make you question the whole set of terms, geek, nerd, dweeb, Dilbert, paste eater. KATHERINE: You're in this band, aren't you? HAL: Okay yes, I play the drums.
|
Flat and Flatter. Ian Stewart's new book
``Flatterland: Like Flatland Only More So'' (Perseus)
is reviewed in the 17 May 2001 Nature. The review,
by Lisa Lehrer Dive (Department of Philosophy, Sydney) and
Andrew Irvine (Department of Philosophy, UBC) praises Stewart's
versatility in conjuring up examples to show ``just how
fundamental mathematics is, and how everything around us, indeed
everything we can think of, may be formed and discussed in mathematical
terms.'' Stewart follows Edwin Abbott's lead in using the adventures
of human-like characters (Vicki Line meets the Space Girls: Curvy Space,
Bendy Space, Pushy Space, Squarey Space and Minny Space) to lead the
reader through unfamiliar mathematical territory. ``Cleverly and
enganingly, he opens our minds to the possibility that, just as
the Flatlanders' conception of rheor world was inadequate for an
understanding of what space is really like, so too, our view of
space as three `flat' dimensions and a single temporal one is only
the tip of the iceberg.''
Why don't we have six limbs? This is one of the questions
considered by David Ruelle in a ``concept'' piece ``Here be no
dragons'' in the 3 May 2001 Nature. The piece is mostly an
introduction to chaos, but he goes on to digress ``on the tantalizing topic
of historical probabilities.'' ``To take a concrete example, instead of asking
when biological evolution decided that terrestrial vertebrates have four
limbs, we might ask what the probability was that at some prescribed
earlier time, say the end of the Cambrian, they would develop six limbs.''
He mentions possibly useful adaptations of the extra limbs for
manipulation (centaurs) or for flying (dragons). More generally, he
brings up the question of ``how life on Earth would have evolved if the
great cataclysm and extinction at the end of the Cretaceous had not
taken place,'' and suggests that some day we may understand enough
about biological evolution to estimate the probabilities involved.
Nature illustrated the piece with Leonardo's ``Fight between
a dragon and a lion,'' but Leonardo had voted for four: his dragon
is organized along the lines of a bat.
Complexity too simple? The May 11, 2001 Chronicle of Higher
Education ran a long piece by Richard Monastersky reporting on the
controversy raging on the borders of paleobiology and mathematics. It
starts with Per Bak (Department of Mathematics,
Imperial College of Science, Technology, and Medicine,
London), who published How Nature
Works: The Science of Self-Organized Criticality (Copernicus) in
1996. The title alone was enough to ruffle feathers. Bak claimed that
populations of species are governed by the dynamical theory of
Self-Organized Criticality (S.O.C.), and that large fluctuations in
the fossil record can be explained by the same kind of laws that
govern the birth and death of avalanches in a sand pile. His evidence
is that these fluctuations obey a power law. Monastersky quotes Bak:
"I do think that's how it works, because it has the
fingerprint of this phenomenon. That's not a
proof, but at the very least people should think about [the
possibility] that mass extinctions are intrinsic to the way
that evolution works and do not need an external cataclysmic
effect." The reaction has been bitter.
``That's
logic on the same level as saying, `Bears like honey, my wife
likes honey, therefore my wife is a bear.'" This from Mark
Newman, another professor at the Santa Fe Institute, where Bak
also holds a chair. But Newman concedes that the impact of S.O.C.
has stimulated new angles of research in paleobiology.
Monastersky concludes with the thought
that even if S.O.C. theory does not survive in paleobiology,
``it has left behind some
intellectual progeny that continue to compete in the harsh
world of evolutionary studies.''
Newton vs. Leibniz on the air. If you were listening
to WSHU/WSUF in Fairfield CT Friday May 25 you would have heard an
episode of John Lienhart's radio column Engines of our Ingenuity
devoted to Leibniz (dx/dt) and Newton (x-dot)
and their priority
controversy over the invention of the Calculus (which has been
called the war between deity and dotage). Lienhart bases his story on the
episode as recounted in Hal Hellman's Great Feuds in Science
(Wiley, 1998,1999). Newton's forces won the war:
``Leibniz died poor and dishonored, while Newton was given a state
funeral.'' But Leibniz'
conception of Calculus, encapsulated in the brilliantly apposite
notation he invented and that we use today, has flourished
alongside Newton's. His reputation survived his propaganda defeat and
his lampooning by Voltaire; he ``gradually finds his place as one
of the greatest thinkers of all time.'' This episode, #1375, is
available online.
Physiological rhythms. Nature for 8 March 2001 featured a review article
``Synchronization and rhythmic processes in physiology'' by
Leonard Glass of the McGill Physiology Department. (The item was also
picked up in the April 13 Science-Week.)
Glass gives a wide survey of the area, with many detailed examples, and
giving special emphasis to the important roles played by chaos and noise.
He calls attention to the existing lag between the development
of mathematical understanding of dynamical systems and the implementation
of that understanding in physiological and clinical practice, but also to
the size of the theoretical task ahead. ``In the
physical sciences, scientific understanding has been expressed in elegant
theoretical constructs and has led to revolutionary technological innovation. If the
advances in understanding physiological rhythms will follow the same trajectory,
then we are still just at the beginning.''
Beyond the spherical cow is not the title of a
surrealist painting but of a ``news and views'' piece by John Doyle
(CalTech) in the 10 May 2001 Nature. The spherical cow comes
from the old joke about the theoretical physicist
presenting his solution to the problem of increasing milk production.
``First,''
he begins, ``we assume a spherical cow.'' Doyle is reporting on the
First International Symposium on Computational Cell Biology (March 4-6, 2001)
and concludes: ``A prominent theme was that biology needs more theory,
in additional to modeling and computation, to make sense of complex
networks.''
-Tony Phillips
Stony Brook
|
|
Comments:webmaster@ams.org
© Copyright 2001, American Mathematical Society |