
The Differential Geometry of the Sphericon
3. Using Gauss' Theorem to measure surface curvature
Here is Gauss' Theorem: If a geodesic polygon with n sides
encloses an area A, then (in radian measure) the sum of its interior
angles minus (n-2) is equal to the total curvature of A.
is equal to the total curvature of A.
Examples:
- For a planar polygon the curvature is zero everywhere so the
total curvature is zero. Gauss' Theorem reduces to the fact that
for such a polygon the sum of the angles is (n-2)
 . Special case:
sum of angles in a triangle is
. Special case:
sum of angles in a triangle is  .
.
- The general definition of total curvature uses an integral,
but when the curvature has the constant value K,
the total curvature is just K times the area of A.
- A sphere of radius R has constant curvature
1/R2. The 0 and 90-degree meridians and the equator
form a geodesic triangle (n=3) with three right angles. The area
of this triangle is one-eighth of the area of the sphere, or
(1/8)x(4
 R2) =
R2) =  R2/2. The total curvature is then
R2/2. The total curvature is then
 R2/2 x 1/R2 =
R2/2 x 1/R2 =  /2. Which is equal to the sum of the
interior angles minus
/2. Which is equal to the sum of the
interior angles minus  .
.
The two-dimensional geographers living on their surface can
measure curvature safely by enclosing a curved region in a
geodesic polygon and adding up the interior angles. Suppose,
for example, their surface had a region with the geometry of
a cone. To be specific, we make a cone by taking a pie-slice
(good to be generous here) with vertex angle 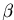 and gluing
the edges together.
and gluing
the edges together.
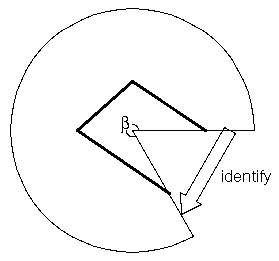
Our geometers living on the cone have to avoid the cone point:
their insides would be stretched by a factor of 2 /
/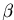 . Imagine
that they draw a geodesic triangle around the cone point.
. Imagine
that they draw a geodesic triangle around the cone point.
- Suppose for
simplicity that one of the vertices of the polygon is on the line
there the two sides of the pie-slice are stuck together. Since
the cone does not stretch when unrolled into the pie-slice,
the triangle unrolls into a 5-sided polygonal figure.
- The sum of the interior angles
of this figure is exactly the sum of the angles of the triangle
plus
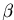 (two of the angles of the figure coalesce into one
of the angles of the triangle when the cone is reassembled).
(two of the angles of the figure coalesce into one
of the angles of the triangle when the cone is reassembled).
- Since the sum of the interior angles in a planar 5-sided
polygon is (5-2)
 = 3
= 3 , the sum of the interior angles in the
original triangle is 3
, the sum of the interior angles in the
original triangle is 3 -
-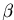 .
.
- Gauss' Theorem tells us that
the enclosed curvature in the geodesic triangle is the sum
of its angles minus
 , yielding 2
, yielding 2 -
- 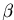 as the
total curvature inside the triangle.
as the
total curvature inside the triangle.
- This argument is
independent of the size of the triangle. In particular,
it holds no matter how small the triangle is. This means that
the cone has curvature 2
 -
-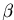 concentrated at the cone-point.
concentrated at the cone-point.
By using Gauss' Theorem, the surface geographers have made this
determination without ever touching the cone point itself.
On to Sphericon page 4.
Back to Sphericon page 2.
© copyright 1999, American Mathematical Society.
 . Special case:
sum of angles in a triangle is
. Special case:
sum of angles in a triangle is  .
.
 R2) =
R2) =  R2/2. The total curvature is then
R2/2. The total curvature is then
 R2/2 x 1/R2 =
R2/2 x 1/R2 =  /2. Which is equal to the sum of the
interior angles minus
/2. Which is equal to the sum of the
interior angles minus  .
.

 is equal to the total curvature of A.
is equal to the total curvature of A. . Special case:
sum of angles in a triangle is
. Special case:
sum of angles in a triangle is  .
.
 R2) =
R2) =  R2/2. The total curvature is then
R2/2. The total curvature is then
 R2/2 x 1/R2 =
R2/2 x 1/R2 =  /2. Which is equal to the sum of the
interior angles minus
/2. Which is equal to the sum of the
interior angles minus  .
.
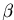 and gluing
the edges together.
and gluing
the edges together.

 /
/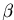 . Imagine
that they draw a geodesic triangle around the cone point.
. Imagine
that they draw a geodesic triangle around the cone point.
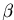 (two of the angles of the figure coalesce into one
of the angles of the triangle when the cone is reassembled).
(two of the angles of the figure coalesce into one
of the angles of the triangle when the cone is reassembled).
 = 3
= 3 , the sum of the interior angles in the
original triangle is 3
, the sum of the interior angles in the
original triangle is 3 -
-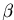 .
.
 , yielding 2
, yielding 2 -
- 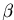 as the
total curvature inside the triangle.
as the
total curvature inside the triangle.
 -
-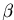 concentrated at the cone-point.
concentrated at the cone-point.