This fact should be plausible, and can be proved by a straightforward calculation as follows.

Parametrize the 2-sphere S² of radius 1 by $\theta,\phi$ (longitude,co-latitude). Then the usual metric is

$$ds^2 = d\phi^2 + \sin^2\phi d\theta^2.$$
Note that the curves $\theta=$constant are great circles.

Parametrize C= the cone on S² by $\theta,\phi,r$ where r is the distance from the cone point. Then the usual metric on C (with the cone point at distance k from the sphere) is

$$ds^2 = dr^2 + (r^2/k^2)(d\phi^2 + \sin^2\phi d\theta^2).$$

A curve $\gamma\colon [0,1]\rightarrow C$ will have coordinates $\theta(t),\phi(t),r(t)$ for t in [0,1]. If the curve is differentiable, its length is

$$L(\gamma)=\int_0^1\sqrt{(\frac{\textstyle dr }{\textstyle dt}... ...+ \sin^2\phi (\frac{\textstyle d\theta}{\textstyle dt})^2]}~dt.$$

Suppose the curve joins two points in the cone over the great circle $\theta=\theta_0$, i.e. that $\theta(0)=\theta(1)=\theta_0$. 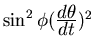Then the curve $\bar{\gamma}$ given by $\bar{\gamma}(t)= \theta_0,\phi(t),r(t)$, which lies entirely in the cone over the great circle $\theta=\theta_0$, will have same endpoints as $\gamma$ and will be shorter, since all the terms in the length integral were positive, and the term $\sin^2\phi (\frac{\textstyle d\theta}{\textstyle dt})^2$ will now be zero.

The path of a light ray is the curve of shortest length between its endpoints. So if $\gamma$ is the path of a light ray between two points in the cone over a great circle, then $\gamma$ must lie entirely in that cone.

Back to Gravitational Lensing and Geometric Lensing.