This sequence of pictures, dating back to 1966, may still be the best way I have to communicate the sphere eversion based on a double-covering of an immersion (Boy's Surface) of the projective plane. They come from my original submission to Scientific American and were marked up by the reviewer there; image h was used for their cover in May of that year.
For definitions, and for the history of this eversion, which involves Steve Smale, Heinz Hopf, Niko Kuiper and René Thom, see the first few slides of 50+ years of sphere eversions.
In these images, the two sides of the sphere are not colored differently; instead, color is used to connect elements of the surface from one level to another, and to follow them from one stage to another, starting with stage f.
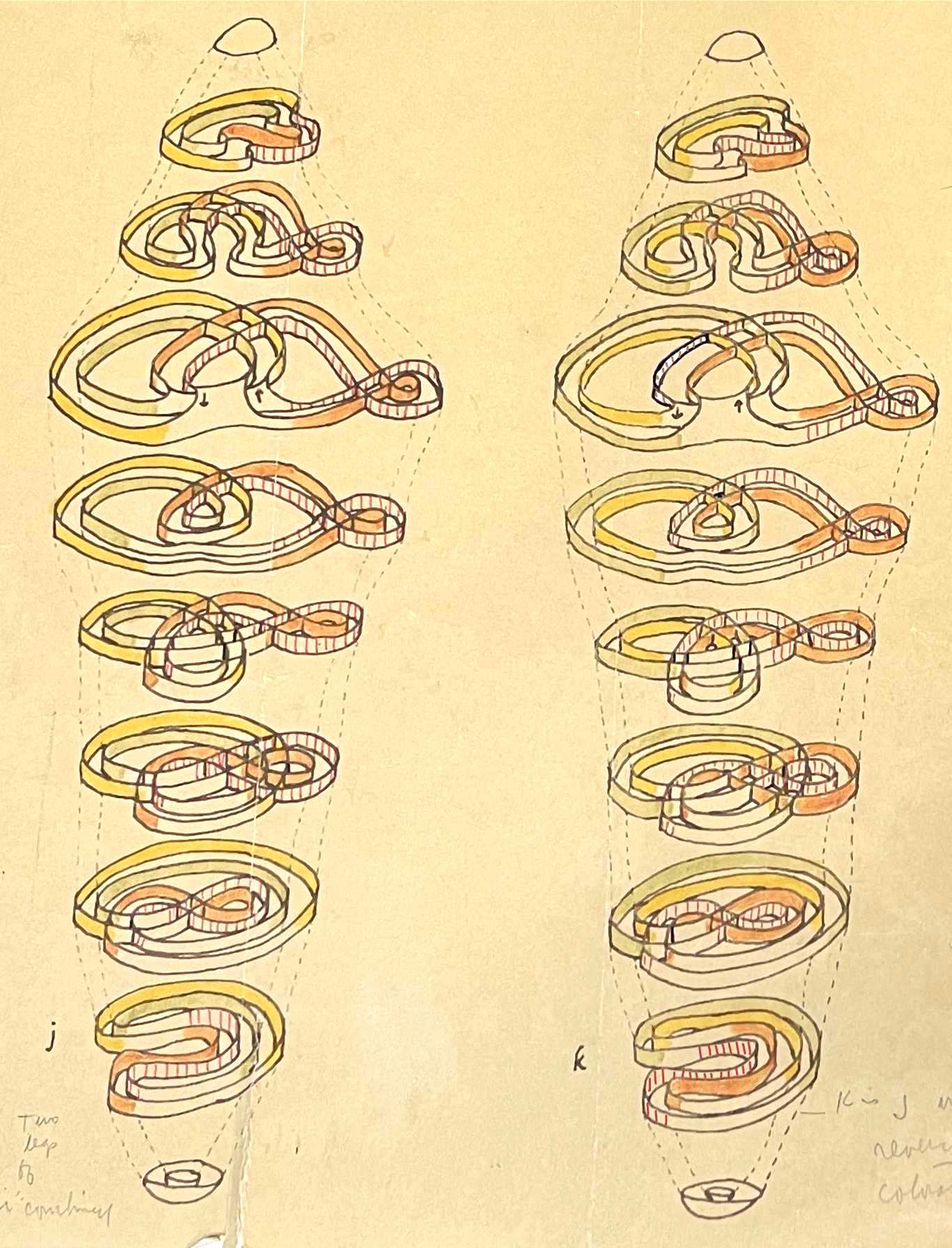 Images j and k show the sphere as a double-covering of
Boy's Surface; between j and k,
the two layers have moved through each
other. The picture looks the same except the colors have all been
exchanged. Now the eversion proceeds by following the steps backward
from i to a, with the new colorings.
Images j and k show the sphere as a double-covering of
Boy's Surface; between j and k,
the two layers have moved through each
other. The picture looks the same except the colors have all been
exchanged. Now the eversion proceeds by following the steps backward
from i to a, with the new colorings.
These sketches were exhibited at the Walker Art Center, Minneapolis, in the show The Quick and the Dead curated by Peter Eleey, Apr 24-Sep 27, 2009.
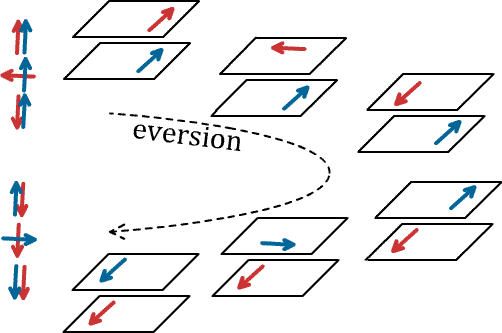
Note that during the eversion a vector on the (originally) upper saddle will have rotated 360$^\circ$ with respect to one on the lower.
 Anthony Phillips
Anthony Phillips