What is the Binary Tetrahedral Group?

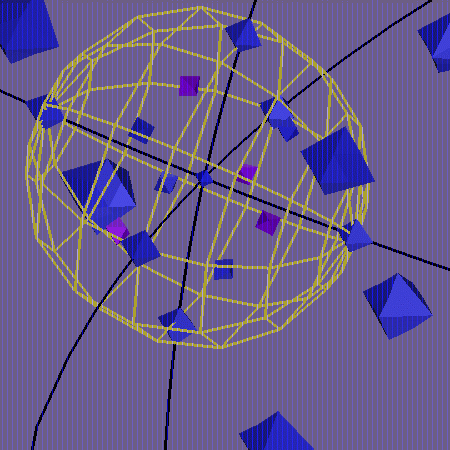This picture shows the Binary Tetrahedral Group embedded as a subgroup of the matrix group SU(2). SU(2) is geometrically a 3-dimensional sphere of radius one; here we see a conformal projection of that sphere into 3-space. The point 1 is at the intersection of the three black circles of longitude. The six points $\pm \mathbf{i},\mathbf{j},\mathbf{k}$ at the intersections of these circles with the yellow equatorial sphere. Eight other group points lie inside the sphere, at a distance $\frac{\pi }{3}$ from 1. They are $a,b,c,d$ (colored violet) and $-a^2,-b^2,-c^2,-d^2$. Six of the nine points outside the equatorial sphere are visible here. They appear larger because they are closer to the projection point (near $-1$). The image of the point $-1$ itself has been suppressed. It would occupy the whole background. This image was produced, using GeomView modules developed at the Geometry Center, by Summer Institute student Rebecca Frankel.

The Tetrahedral Group is the group of orientation- preserving symmetries of an equilateral tetrahedron. If the vertices of the tetrahedron are labeled A,B,C,D, each of the symmetries may be represented as a permutation of these four symbols. Each even permutation corresponds to an orientation-preserving symmetry. The twelve are

• the identity
• eight rotations about axes going through a vertex and the opposite face. There are four vertices; each rotation can be by 120${}^{\circ }$ or 240${}^{\circ }$
  (ABC), (ACB), (ABD), (ADB), (ACD), (ADC), (BCD), (BDC),
• three 180${}^{\circ }$ rotations about axes joining the midpoints of two opposite edges:
  (AB)(CD), (AC)(BD), (AD)(BC).

The Special Unitary group SU(2) consists of 2 by 2 complex matrices of the form $$\left(\begin{array}{cc}(x+iy)& (z+iw)\\ (-z+iw)& (x-iy)\end{array}\right)$$ with determinant $x^2+y^2+z^2+w^2=1$. There is a group homomorphism SU(2) $\to$ SO(3) which can be described in terms of $x,y,z,w$ but which can be more geometrically defined using quaternions. A quaternion can be identified with a matrix like the one above, but without the determinant condition in general. The quaternionic notation for that matrix is $\mathbf{1}x+\mathbf{i}y+\mathbf{j}z+\mathbf{k}w$, where $\mathbf{1},\mathbf{i},\mathbf{j},\mathbf{k}$ correspond to the matrices $$\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}i& 0\\ 0& -i\end{array}\right),\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),\left(\begin{array}{cc}0& i\\ i& 0\end{array}\right)$$ respectively. The rules for multiplying quaternions follow from the rules for matrix multiplication; equivalently: ${\mathbf{i}}^2={\mathbf{j}}^2={\mathbf{k}}^2=-\mathbf{1}$, $\mathbf{i}\mathbf{j}=-\mathbf{j}\mathbf{i}=\mathbf{k},$ $\mathbf{j}\mathbf{k}=-\mathbf{k}\mathbf{j}=\mathbf{i}$, $\mathbf{k}\mathbf{i}=-\mathbf{i}\mathbf{k}=\mathbf{j}$, extended linearly. The condition $x^2+y^2+z^2+w^2=1$ defines a unit quaternion. Since the matrix corresponding to the unit quaternion $\mathbf{1}x+\mathbf{i}y+\mathbf{j}z+\mathbf{k}w$ has unit determinant, its inverse is exactly $$\left(\begin{array}{cc}(x-iy)& (-z-iw)\\ (z-iw)& (x+iy)\end{array}\right)$$ so the multiplicative inverse of the unit quaternion $\mathbf{1}x+\mathbf{i}y+\mathbf{j}z+\mathbf{k}w$ is $\mathbf{1}x-\mathbf{i}y-\mathbf{j}z-\mathbf{k}w$.

The vector $(a,b,c)$ in ${\mathbf{R}}^3$ can be identified with the pure imaginary quaternion $a\mathbf{i}+b\mathbf{j}+c\mathbf{k}$; then each quaternion $\mathbf{q}$ defines a linear map $L(\mathbf{q}):{\mathbf{R}}^3\to {\mathbf{R}}^3$ by $L(\mathbf{q})(a\mathbf{i}+b\mathbf{j}+c\mathbf{k})=\mathbf{q}\times (a\mathbf{i}+b\mathbf{j}+c\mathbf{k})\times {\mathbf{q}}^{-1}$, using quaternionic multiplication. It is straightforward to check that $L(\mathbf{q})$ is also pure imaginary; the fact that the determinant of a product is the product of the determinants then guarantees that $L(\mathbf{q})$ is a length-preserving, and therefore orthogonal, transformation; the question of orientation can be answered by noting that $L(1)$ is the identity and that SU(2) is connected. Also, the definition yields immediately that $L$ is a homomorphism from SU(2) to SO(3): $L(\mathbf{p}\mathbf{q})=L(\mathbf{p})L(\mathbf{q})$ for any two unit quaternions $\mathbf{p}$ and $\mathbf{q}$. Finally, two unit quaternions $\mathbf{p}$ and $\mathbf{q}$ give the same SO(3) element if and only if $\mathbf{p}=\pm \mathbf{q}$; the condition is equivalent to the three equations $L({\mathbf{q}}^{-1}\mathbf{p})\mathbf{i}=\mathbf{i}$, $L({\mathbf{q}}^{-1}\mathbf{p})\mathbf{j}=\mathbf{j}$, $L({\mathbf{q}}^{-1}\mathbf{p})\mathbf{k}=\mathbf{k}$; writing ${\mathbf{q}}^{-1}\mathbf{p}=\mathbf{1}x+\mathbf{i}y+\mathbf{j}z+\mathbf{k}w$ in these three equations yields $x^2=1$, $y=z=w=0$, so ${\mathbf{q}}^{-1}\mathbf{p}=\pm 1$, i.e. $\mathbf{p}=\pm \mathbf{q}$.

For obvious reasons, then, the map $L$ is called the double-covering homomorphism from SU(2) to SO(3). Since the tetrahedral group is a 12-element subgroup of SO(3), the SU(2) matrices which map to elements of the tetrahedral group will form a 24-element subgroup of SU(2). This is the Binary Tetrahedral Group.

Click here for an explicit description of the elements of the Binary Tetrahedral Group in terms of quaternions.

Reset using LaTeX, 3/6/23.

Back to Bimary Tetrahedral Main Page
Back to Tony's Home Page