and 
are
smoothly homotopic, then 
.
Week 9 - Part 1 (For a text-only page click here.)
1. Elements of de Rham cohomology. There are two results which allow our elementary calculations for the point and the circle to be extended to a large collection of manifolds.
Homotopy Theorem. If and are
smoothly homotopic, then .
Mayer-Vietoris Theorem. Suppose a manifold M
can be written as a union of two open sets U and V. Then
there exist a set of linear 
which fit, together with the maps induced by the inclusions
, 
,
,
, into an exact sequence (the
Mayer-Vietoris sequence)
Example. Calculation of 
. We will need the following
easy consequence of the Homotopy Theorem: if 
as
smooth deformation retract, then 
is an isomorphism.
Let U and V be the complements of the North and South poles
respectively; then U and V are open discs and 
is
an open annulus. The discs have points as deformation retracts,
and the annulus has a circle, so using the homotopy theorem we
know 
, 
and 
in the Mayer-Vietoris sequence.
We need the additional elementary piece of information: 
.
Then the beginning of the sequence is
i.e.
Exactness implies that the map 
is onto and therefore
that the map 
is the zero map. The next map in the
sequence
i.e.
must therefore be injective, so 
. In the next part of the
sequence
i.e.
exactness implies 
.
Class exercise: Use the same method to calculate 
.
The homotopy theorem.
Proposition A: Let 
be the inclusions at levels 0 and 1. So
, 
. Then
Note: this proposition implies the homotopy theorem, if we
take as definition of smooth homotopy between and 
the
existence of 
with 
and
.
Because then 
and 
, so that
.
Proof of Proposition A. A local coordinate
system 
on M gives a local coordinate system
on 
. In terms of these coordinates,
any p-form on may be written as 
, where the multi-index I ranges over
all p-tuples 
, and the multi-index J
ranges over all (p-1)-tuples 
. For
for such an I, 
means 
, and
similarly for J.
Let the linear map 
be defined by
, with
as above. First we check that this definition is
independent of the choice of coordinate system . In another
system 
suppose 
. The change of coordinates from
the (t,u) system to the (t,v) system has the form
i.e. the t's and the other coordinates transform independently.
Consequently 
where the 
are
appropriate 
minors of the matrix 
; and similarly
for 
; so calculating 
in the v-cordinates
gives
this last step because the are constant in t,
the same as the calculation in the u-coordinates. Next we verify the formula
. In fact,
so
On the other hand
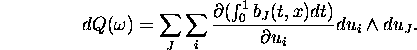
Interchanging differentiation with respect to 
and
integration with respect to t makes this term equal and
opposite to the second term in 
. So
Now the inclusion 
clearly satisfies 
and 
; consequently 
; similarly
. This proves the
formula.Finally suppose is a closed form representing
a class in 
; since 
, the formula
gives 
;
the two pulled-back forms differ by a coboundary: they are
in the same cohomology class.
Back to Main Toplogy-Geometry II Page.
Back to Tony's Home Page.