Stony Brook University       MAT 336       History of Mathematics

Spherical Trigonometry and Navigation

1. Spherical Trigonometry deals with spherical triangles. On a sphere, the role of straight lines is played by great circles. Each of these is the intersection of the sphere with a plane passing through its center. Line segments become great circle arcs. If the sphere has radius R, so will all its great circles; so the length of an arc is exactly R times the radian measure of the central angle it intersects (or R times (π/180) times the measure of that angle in degrees).
    In navigation, for most purposes the surface of the Earth can be considered a sphere. The distance between points X and Y on the Earth is the length of the great-circle arc between them. This length can be expressed essentially as an angle through the convention that 1 nautical mile is 1 minute (1') of arc (i.e. 1/60 of one degree) along a great circle.
    For example, the distance from the North Pole to a point on the Equator is 1/4 of a great circle: 90o or 90x60=5400' which gives 5400 nautical miles. The radius of the Earth is built into the conversion factor between nautical miles and kilometers: 1 nautical mile = 1.852 km.
    The upshot is that calculating the distance between two points amounts to calculating the central angle they determine on the great circle that passes through both of them. This is where spherical trigonometry becomes useful.

2. "In book XI of [Ptolemy's] Almagest the principles of spherical trigonometry are stated in the form of a few simple and useful lemmas; plane trigonometry does not receive systematic treatment..." [1]. This is because of the great importance of spherical trigonometry for astronomy. We have seen how Aryabhata (456-550) tabulated sines. The next great progress came with Al-Battani (or, Albategnius; c.868-929), the greatest Islamic mathematician and astronomer of his time. He used the function sinvers defined by sinvers(α) = 1 - sin(π/2 - α) essentially equivalent to our cosine, in astronomical calculations; but despite insinuations to the contrary (e.g. in [1]), he did not formulate the law of cosines for a spherical triangle. The first formulation we know, still in terms of sinvers, is due to Regiomontanus (1464). Details from [3] are summarized in The True History of the Law of Cosines.

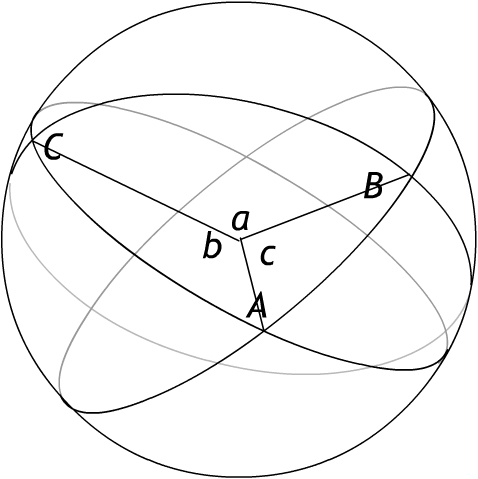
The the spherical law of cosines states, for a spherical triangle with surface angles A, B, C opposite sides corresponding to central angles a, b, c, that

cosa = cosb cosc + sinb sinc cos A.


3. This law has the planar law of cosines as limit when a, b, and c tend to zero. Use the approximations cosa = 1 - (1/2)a2, etc., and sinb = b, etc. valid for small a, b, c, and discard the higher-order term (1/4)b2c2.

4. When we locate a point X on the Earth by giving its latitude and longitude, we are giving angular coordinates. Latitude is the size of the central angle, along a meridian (the great circle through X and the North Pole P), between X and the equator. The latitude is specified as North (N) for points above the equator, and South (S) for points below, and runs from 0o to 90o. New York City is at latitude 40o47'N, Moscow is at latitude 55o45'N and Buenos Aires is at latitude 34o35'S. (Sometimes latitude is counted negative for points in the Southern Hemisphere). Longitude is the size of the surface angle, at the North Pole, between the "Prime Meridian" (the meridian through Greenwich, England) and the meridian through X. It is measured East (E) or West (W) and runs in each direction from 0o to 180o. New York City is at longitude 73o58'W, while Moscow is at 37o42'E and Beijing is at 113o20'E.

5. Suppose we want to calculate the air distance from New York to Moscow. We know their coordinates.
New York: Latitude l1 = 40o47'N, Longitude L1 = 73o58'W
Moscow: Latitude l2 = 55o45'N, Longitude L2 = 37o42'E. We can mark these coordinates on a globe:
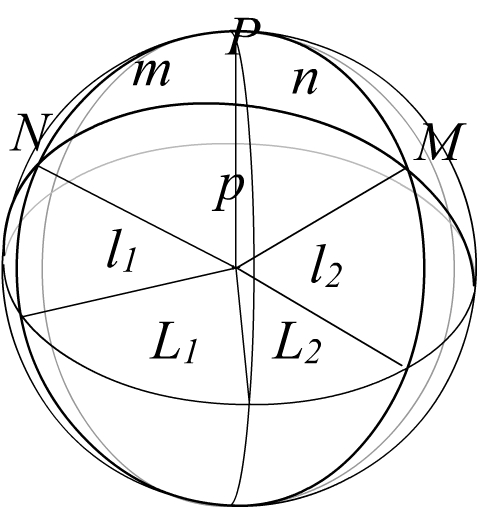New York (N), Moscow (M) and the North Pole (P) are the vertices of a spherical triangle; we label the sides (central angles) oppsite the vertices by n, m, p . We know side m: it is m = 90o - l1 = 49o13'.
Similarly side n is n = 90o - l2 = 34o15'.
We also know the face angle at P: it is the sum of the two longitudes, since one is East and the other is West: P = L1 + L2 = 111o40'.
In this context, the law of cosines gives: cosp = cosm cosn + sinm sinn cos P.
Using a calculator, we find cosp = 0.6532x0.8266 + 0.7572x0.5629x(-0.3692) = 0.3826, and arccos(0.3826) = 67.51o=4050.4'. This gives the great-circle distance from New York to Moscow as 4050 nautical miles, or 7501km.


Exercises:
  1. Calculate the great-circle distance from New York to London (Latitude = 51o32'N, Longitude = 0o5'W). Note that in this case the longitudes are both West and must be subtracted.
  2. Calculate the great-circle distance from Anchorage, Alaska (Latitude = 61o10'N, Longitude = 150o1'W) to Moscow.
  3. What is the maximum latitude along the New York-Moscow great-circle route? (Hint: it occurs at the vertex V of the route, the point where the route makes a right angle with a meridian). You will need to solve for surface angle M by a second application of the law of cosines; then use the spherical law of sines sinA/sina = sinB/sinb = sinC/sinc to solve the rectangular spherical triangle MPV .
  4. [2] Find the initial course and the distance for a voyage along a great circle from Los Angeles (l = 34o03'N, L = 118o15'W) to Aukland (l = 41o18'S, L = 174o51'E). [The initial course is "the angle of departure, measured from the north around through the east [i.e. measured clockwise] from 0o to 360o"[2].] Answer: Course = 224o 8' 48", distance = 5832 miles.
  5. [2] Find the distance by great circle from New York (l1 = 40o40'N, L1 = 4h 55m 54"W) to Cape of Good Hope (l2 = 33o56'S, L2 = 1h 13m 55"E). [Longitude is given here in hours, minutes and seconds of time. Because of the rotation of the Earth with respect to the Sun, 1o of longitude corresponds to a 4m time difference.] Answer: 6779.9 miles.
[1] Ernest William Hobson, Entry "Trigonometry" in the Encyclopedia Brittanica, 11th Edition (1910-1911).
[2] Kells, Kearn and Bland, Plane and Spherical Trigonometry, McGraw-Hill, New York, 1940. This textbook was used at the United States Naval Academy.
[3] Anton von Braunmühl, Vorlesungen über Geschichte der Trigonometrie, Vol. 1, 1900.

Corrected Dec 6, 2006.