2. "In book XI of [Ptolemy's] Almagest the principles of spherical
trigonometry are stated in the form of a few simple and useful lemmas;
plane trigonometry does not receive systematic treatment..." [1]. This
is because of the great importance of spherical trigonometry for
astronomy. We have seen how Aryabhata (456-550) tabulated sines. The
next great progress came with Al-Battani (or, Albategnius; c.868-929),
the greatest Islamic mathematician and astronomer
of his time. He used the function sinvers defined by
sinvers(α) = 1 - sin(π/2 - α) essentially equivalent
to our cosine, in astronomical calculations; but despite insinuations to
the contrary (e.g. in [1]), he did not formulate the law of cosines
for a spherical triangle. The first formulation we know,
still in terms of sinvers, is due to
Regiomontanus (1464). Details from [3] are summarized in
The True History of the Law
of Cosines.

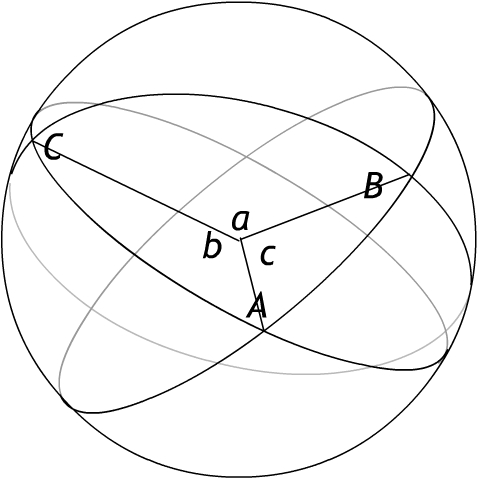
The the spherical law of cosines states, for a spherical triangle with surface angles A, B, C opposite sides corresponding to central angles a, b, c, that
3. This law has the planar law of cosines as limit when
a, b, and c tend to zero. Use
the approximations cosa = 1 - (1/2)a2, etc.,
and sinb = b, etc. valid for small a, b, c, and
discard the higher-order term (1/4)b2c2.
4. When we locate a point X on the Earth by giving its latitude and longitude, we are giving angular coordinates. Latitude is the size of the central angle, along a meridian (the great circle through X and the North Pole P), between X and the equator. The latitude is specified as North (N) for points above the equator, and South (S) for points below, and runs from 0o to 90o. New York City is at latitude 40o47'N, Moscow is at latitude 55o45'N and Buenos Aires is at latitude 34o35'S. (Sometimes latitude is counted negative for points in the Southern Hemisphere). Longitude is the size of the surface angle, at the North Pole, between the "Prime Meridian" (the meridian through Greenwich, England) and the meridian through X. It is measured East (E) or West (W) and runs in each direction from 0o to 180o. New York City is at longitude 73o58'W, while Moscow is at 37o42'E and Beijing is at 113o20'E.
5. Suppose we want to calculate the air distance from New York
to Moscow. We know their coordinates.
New York: Latitude l1 = 40o47'N,
Longitude L1 = 73o58'W
Moscow: Latitude l2 = 55o45'N,
Longitude L2 = 37o42'E. We can mark
these coordinates on a globe:
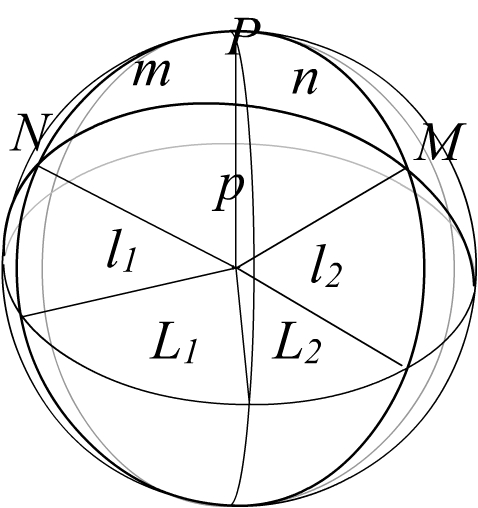 New York (N), Moscow (M) and the North Pole (P)
are the vertices of a spherical triangle; we label the sides (central
angles) oppsite the vertices by n, m, p . We know side m:
it is
m = 90o - l1 = 49o13'.
New York (N), Moscow (M) and the North Pole (P)
are the vertices of a spherical triangle; we label the sides (central
angles) oppsite the vertices by n, m, p . We know side m:
it is
m = 90o - l1 = 49o13'.
Similarly side n is
n = 90o - l2 = 34o15'.
We also know the face angle at P: it is the sum of
the two longitudes, since one is East and the other is West:
P = L1 + L2 = 111o40'.
In this context, the law of cosines gives:
cosp = cosm cosn + sinm sinn cos P.
Using a calculator, we find
cosp = 0.6532x0.8266 + 0.7572x0.5629x(-0.3692) = 0.3826, and
arccos(0.3826) = 67.51o=4050.4'. This gives the great-circle
distance from
New York to Moscow as 4050 nautical miles, or 7501km.
Corrected Dec 6, 2006.