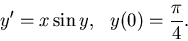My NAME is:

MAT 132 Calculus II

Midterm 2

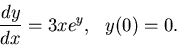
November 15, 2000

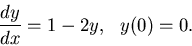
CALCULATOR POLICY:

The following calculators are allowed to be used on this examination: TI-81, 82, 83, 85, 86; Sharp EL-8200, EL-8200C. Any other calculator is subject to confiscation, and its user may be accused of cheating.
ONLY programs distributed in connection with MAT 131 and 132 may be stored in the calculators. Any other use of calculator memory to store information relevant to this examination will be considered cheating.

Show all your work on these pages! Total score = 100

(30 points) Solve the following initial value problems, where y is an unknown function of x. Show all your work.
- (a)
- (b)

(30 points)

The tank is in the shape of a cone.

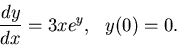
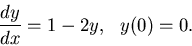
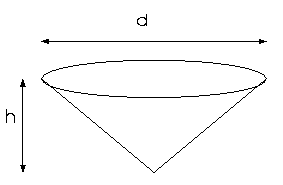
A tank is in the form of a right circular cone with the point down. The base of the cone is d = 6m in diameter, and the height of the cone is h = 3m. The tank is filled with water (density 1000kg/m³). Calculate the work it takes to empty this tank by pumping the water out over the top. A kilogram at the surface of the Earth weighs 9.81 newtons .

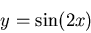(10 points) Solve the equation (x+iy)(3-i)=6.

(10 points) Set up the integral giving the length of the graph of

between x=0 and

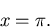
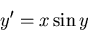(20 points)

(a) In the diagram below sketch in the slopefield at the 9 gridpoints shown, for the differential equation .
Draw appropriate slopes at the 9 gridpoints shown.
(b) Use these slopes to sketch an approximate solution to the initial value problem

Posted Dec 4 2000