MAT125 Spring 2011 Review for Midterm I
1.1
Understand the definition of function (box, p.12) and the importance
of the word "exactly." The Vertical Line Test (p.17) shows exactly
what "exactly" means in terms of graphs (Exercises 5-8).
Be able to ascertain the domain of
a function either from the formula (Example 6,
Exercises 29-33)
or the graph
(Example 1,Exercises 1, 2, 5-8).
Practice sketching graphs (Exercises 36-39),
especially for piecewise-defined functions (Exercises 43-46).
1.2 Be familiar with the "essential functions." Linear (Example 1,
Exercises 10,11,15,18); be able to interpret slope and
y-intercept. Polynomial: know what the degree is (p.29),
(Example 4, Exercise 3). Power functions: understand
that the 1/n power (n a positive integer)
corresponds to the nth root; and that if n is
even, f(x) = x1/n is only defined for positive
x; understand negative powers as reciprocals of the positive:
x-n = 1/xn; be comfortable with the law of
exponents in this context: xaxb
= xa+b, xa/xb
= xa-b, (xa)b
= xab; a and b can be integral,
fractional, positive, negative, anything.
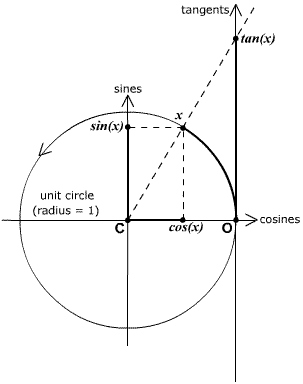 Trigonometric functions: keep this diagram firmly and
permanently in mind to understand sine, cosine and tangent
as functions of x in radians. Starting at O (the right-hand
intersection of the unit circle with
the horizontal axis),
go a distance x
counterclockwise along the circle. Projection onto the horizontal
(cosines)
axis then gives cos(x); projection onto the vertical (sines) axis
gives sin(x); the line through C (center of the circle)
and x intersects the tangents axis at tan(x).
(The tangents axis is tangent to the circle at O.)
Trigonometric functions: keep this diagram firmly and
permanently in mind to understand sine, cosine and tangent
as functions of x in radians. Starting at O (the right-hand
intersection of the unit circle with
the horizontal axis),
go a distance x
counterclockwise along the circle. Projection onto the horizontal
(cosines)
axis then gives cos(x); projection onto the vertical (sines) axis
gives sin(x); the line through C (center of the circle)
and x intersects the tangents axis at tan(x).
(The tangents axis is tangent to the circle at O.)
Elementary properties of sin, cos, tan
can be retrieved from this diagram, e.g. -1 ≤ sin(x) ≤ 1,
-1 ≤ cos(x) ≤ 1, tan(x)
= sin(x)/cos(x) (similar triangles),
sin2(x) + cos2(x) = 1
(Pythagorean theorem), sin(x + 2π) = sin(x),
cos(x + 2π) = cos(x) (2π is length of
circle), etc.
Exponential and logarithmic functions,
also "essential," are covered in § 1.5.
1.3 Understand how translations work (Box, p.38 and Figure 1); remember that
f(x-c) has the graph of f(x) shifted c
units to the right, and understand why! (Exercise 3ade).
Same for stretching and reflecting (Box, p.39 and Figure 2); remember
that for example f(2x) has the graph of f(x)
compressed by a factor of 2, and understand why. Also
understand why -f(x) and f(-x) do very different
things to f(x). Exercises 1,2,3,4,5.
Understand that when two functions are combined by +, x, - and / the
domain of the combination is the intersection of the two domains:
the set of points
where both functions are defined, plus no zeroes in the
denominator! Exercises 29,30. Be able to "complete the
square" (Example 2, Exercise 12).
Remember that in the composition f(g(x)) the function g
is applied first. (Example 6, Exercises 31-36).
1.5 Be able to sketch the graph of an exponential function
f(x) = ax: f(0)= 1 always.
The function
increases from 0 to infinity if a > 1, it's constant
and equal to 1 if a = 1, it decreases
from infinity to 0 if 0 < a < 1. Only positive
a are considered! (Exercises 7,8,9).
Be familiar and completely
comfortable with the Laws of Exponents (box, p.54). Know
what e is (p.57). (Example 4, Exercises 14,15,16).
1.6 Understand that a function can only have an inverse if
it is one-one, i.e. it satisfies the Horizontal Line Test (box, p.61).
Examples 1,2 are fundamental. Exercises 5-8.
Understand and be able to apply the algorithm (box, p.64)
to calculate the inverse of a one-one function. (Example 4,
Exercises 21,22).
In particular the exponential function f(x) = ax
for any a not equal to 1 has an inverse, called
"logarithm to the base a," and written loga.
Understand and be comfortable with the equivalences between
logax = y and x = ay, etc.
(Boxes on p.65!!). Be comfortable with the Laws of Logarithms
(Box, p.65). (Example 6, Exercises 35,36). Know
the natural logarithm ln x = logex, and
know the change-of-base formula logax =
(ln x)/(ln a) (Box, p.67 Example 10 -requires a calculator).
2.1 Be able to sketch secant lines through a point on a curve,
and the tangent line to the curve at that point, and understand
how to use slopes of secants to estimate the slope of
the tangent (Examples 1,2,Exercises 3, 4 -require calculator).
Be able to calculate average velocities from distance-time
data and to use them to estimate instantaneous velocity
(Exercises 6.7).
2.2 Understand that the limit of a function f at a
does not involve the value f(a) (which may not even
be defined). (Definition, p.95). (Example 1). Also
definitions of left- and right-hand limits (Box, p.100 and below).
Be able to
estimate limx->af(x) as well as one-sided
limits from inspection of
the graph of f (Exercises 3,4,5,6,12).
Use the Chapter Reviews for further reviewing.
Chapter 1
- Concept Check 1 through 12.
- True-False 1 through 11.
- Exercises 1 through 16, 18,19,20.
Chapter 2
- Concept Check 1, 2, 3, 4
- True-False 1 through 8.
- Exercises 1 through 18
 Trigonometric functions: keep this diagram firmly and
permanently in mind to understand sine, cosine and tangent
as functions of x in radians. Starting at O (the right-hand
intersection of the unit circle with
the horizontal axis),
go a distance x
counterclockwise along the circle. Projection onto the horizontal
(cosines)
axis then gives cos(x); projection onto the vertical (sines) axis
gives sin(x); the line through C (center of the circle)
and x intersects the tangents axis at tan(x).
(The tangents axis is tangent to the circle at O.)
Trigonometric functions: keep this diagram firmly and
permanently in mind to understand sine, cosine and tangent
as functions of x in radians. Starting at O (the right-hand
intersection of the unit circle with
the horizontal axis),
go a distance x
counterclockwise along the circle. Projection onto the horizontal
(cosines)
axis then gives cos(x); projection onto the vertical (sines) axis
gives sin(x); the line through C (center of the circle)
and x intersects the tangents axis at tan(x).
(The tangents axis is tangent to the circle at O.)