MAT118 Review for Midterm II
Material from Week 3
Understand how to construct Pascal's triangle (see
notes). Understand the
relation between the triangle and the coefficients
in $(a+b)^n$ (Binomial Theorem, in notes).
Be able to explain why the sum of the numbers in row $n$ is $2^n$,
and their alternating sum is $0$.
Material from Week 4
Understand the "dominoes" solution to the Königsberg bridge
problem (see page 389). Be able to determine by inspection if a graph admits
an Euler circuit (no vertices of odd degree; Theorem on page 394),
or if it admits an Euler path (two vertices of odd degree;
Mindscape 21 on page 398).
If a graph admits an Euler circuit, be able to describe the circuit
by numbering the edges and listing them as they occur in the circuit.
Same for an Euler path. See instructions on pages 392-393.
Material from Week 5
Understand that a connected planar graph must satisfy Euler's Theorem:
$V-E+F=2$, where $V$ is the number of vertices, $E$ the number of
edges, and $F$ the number of planar regions separated by the edges
of the graph. Remember to count the outside as one of the regions
(page 404).
Understand that if a planar graph has $C$ connected pieces, then
it satisfies $V-E+F=C+1$ (Mindscapes 26, 27, 28 page 411).
Understand the correspondence between the vertices, edges and regions
of a planar graph and the vertices, edges and faces of a graph
drawn on a sphere (page 406). So these must satisfy $V-E+F=2$.
Understand how all five regular polyhedra correspond to graphs on a
sphere (see Mindscape 25 on page 411); know their names and be able
to check that they satisfy $V-E+F=2$.
Understand how to draw the dual of a planar graph, or of one on a
sphere: a dual-vertex inside each face; a dual-edge between
dual-vertices if the corresponding faces share an edge (the dual-edge
intersects this edge in one point and does not intersect any
other edge); a dual-face corresponding to each vertex: its
dual-edges correspond exactly to the edges issuing from that vertex.
Understand that the dual of a peninsula edge (page 419) is a dual-edge loop
based at the dual-vertex corresponding to the region the peninsula
sticks into. And conversely the dual of a loop is a dual-edge peninsula
with its tip at the dual-vertex corresponding to the region
enclosed by the loop.
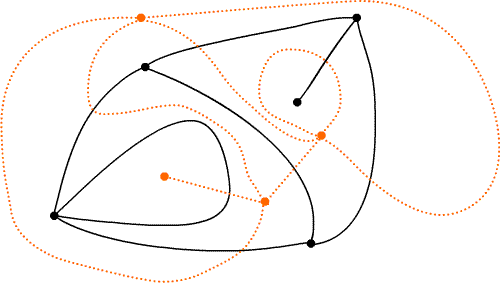
A planar graph and its dual.
Understand that with this construction the dual of a tetrahedron
(4 vertices, 4 triangular faces, each vertex belongs to 3 edges) is again
a tetrahedron. That the dual of a cube (8 vertices, 6 square faces, each
vertex belongs to 3 edges) is an octahedron (6 vertices, 8 triangular faces,
each vertex belongs to 4 edges). And that the
dual of a dodecahedron (20 vertices, 12 pentagonal faces, each
vertex belongs to 3 edges) is an icosahedron (12 vertices, 20 triangular faces,
each vertex belongs to 5 edges). And vice-versa, since the dual of
the dual gets back to the original graph. Duality for regular
polyhedra is explained in section 4.5.
Material from Week 6
Understand that the (3 houses, 3 utilities) problem amounts to asking
if there exists a planar graph with two sets of vertices $A, B, C$
and $X, Y, Z$, and edges $XA, XB, XC, YA, YB, YC, ZA, ZB, ZC$. "Planar"
means in particular that one edge cannot intersect another. (Of course,
they are allowed to meet at vertices). And asking if the pentagram
(5 vertices, all 10 possible edges) can be drawn without edges
intersecting is asking if there exists a planar graph with vertices
$A, B, C, D, E$ and edges $AB, AC, AD, AE, BC, BD, BE, CD, CE, DE$.
Be able to explain why, for a connected, planar graph with no loops
and no multiple edges, the number $E$ of edges and the number $V$
of vertices must satisfy $E \leq 3V-6$ (page 419). This rules out
the pentagram. Also understand that for a bipartite graph
like the (3 houses, 3 utilities) the inequality becomes $E \leq 2V-4$
(page 420). This shows the 3 houses cannot be connected to the
3 utilities without one of the lines crossing. Use Mindscapes 1-16
on pages 428-30 for review.

