Project 2: Fun on a Swing
Due Tuesday, 16 April

Suppose you are a kid (or an adult) who really likes to swing, and your Dad tells you he will make a swing for you, but you have to tell him how high it should be. Since you want to have the most fun possible, you naturally immediately construct a mathematical model and analyze the problem.

For simplicity, we first model the swing as a weightless rod of length l attached at one end carrying a mass m at the other end. Let be the angle the rod makes with the vertical. Then, from physics (using Newton's law force = (mass)(acceleration), for example), we see that the acceleration is given by

where g is the gravitational constant (we use 32 ), is measured in radians, and is the coefficient of friction (which depends on the surface area of the swinger, and the viscosity of air). We can make the substitution to obtain the ``usual'' equations for a damped pendulum

(we have used the common notation to indicate the derivative of with respect to time).

We want this pendulum to be more like a swing, that is, to think of a person sitting on the swing and ``pumping''. To that end, in class we came up with the equations

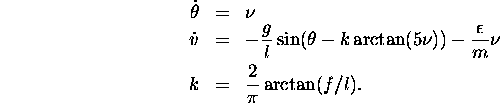
The additional function has been added to account for pumping on the swing; this is the angular amount that the swinger offsets his (or her) center of mass from the seat of the swing. We (perhaps somewhat arbitrarily) settled on the values

to represent a ``typical'' swing (the relevant units here are various combinations of feet, seconds, and radians. The value of epsilon in particular was chosen quite arbitrarily, and may have no actual relationship to reality). You may use other values of the constants if you want, but please point this out in your writeup if you do, and why you think these may be more ``realistic''.

The general problem of the project it to analyze the relationship between the length l of the swing and its behaviour, with a particular eye towards which swings are the most ``fun''.

1. Fixing all of the constants except the length l, what is the longest swing which can go over the top (that is, achieve an angle ), and hence no limit cycle exists. We saw in class that, for the constants chosen above, this is between l=5 and l=10.
2. Again fixing all the constants except l, what is (approximately) the relationship between the maximum (vertical) height one can achieve (starting from a small angle and ) and the length l of the swing? Is there a length of swing that is the ``best'' to use to get the highest off the ground, and if so, what is that height (approximately)?

In your writeup, you should explain what physical quantity each of the terms in the differential equation represents, and in particular why we chose the quantity . You may wish to also describe the behavior of the unforced system (that is, with f=0) first, to make your explanation easier to follow, and perhaps the undamped system ( ) as well. You will probably wish to include graphical output from maple to support your findings; if so, please explain clearly what the picture is of, what each axis represents, and so on. It would be a good idea to relate the pictures directly to the physical motions of the swing, for example, if we see an elliptical object in the a plot of vs. , explain what this means in terms of how the swing is moving.

Feel free to do more than answer the 2 questions; if you've found something interesting you want to explore or explain, please do so. For example,

• What about other measures of ``fun'', for example, what length of swing goes fastest (maximizes the quantity )?
• Suppose that instead of the forcing function above, you use something periodic in time, like (Note that this causes the differential equation to depend on time, so a phase portrait is not meaningful, because solutions can cross in the phase plane. Still, you can analyze what happens to particular solutions (using Runge-Kutta, for example)). What happens for various values of k (fixing everthing else for a while)? What, physically, does this forcing correspond to doing, and what, physically, is the resulting behavior? Is this what you expected?

You might be able to come up with other questions and variations. It would be nice to try.

As always, present your writeup in such a way that someone who has never taken our class or used these computers will understand what you are saying. Think of your intended audience as being, say, a senior math major who is not enrolled in this class. I am more interested in a coherent presentation what what you did and why you did it than in long lists of numbers.

You may work with other members of the class to do your experiments, but please write up your own project. If you work with others for a significant part of the project, it would be nice to say with whom you collaborated.