prove that the origin is an attractor in the future, i.e., every solution verifies
[You can ask around how to do this, but then you have to show clearly that you have understood it.]
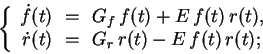
where
First, write some words to explain why these equations make
sense. Then, fix ![]() ,
, ![]() (it's notorius that rabbits
have the tendency to reproduce quickly) and
(it's notorius that rabbits
have the tendency to reproduce quickly) and ![]() . For a few
initial conditions of your choice, plot the trajectories
in the
. For a few
initial conditions of your choice, plot the trajectories
in the ![]() -plane (say, with
-plane (say, with
![]() and
and
![]() ). For the same initial conditions, plot the actual
solutions too (i.e,
). For the same initial conditions, plot the actual
solutions too (i.e, ![]() against
against ![]() , and
, and ![]() against
against ![]() ).
Write some comments interpreting how the behaviour of the solutions
relates to what happens to the two species.
).
Write some comments interpreting how the behaviour of the solutions
relates to what happens to the two species.
Finally, repeat the same procedure with ![]() . Things change
substantially. Again, what is the ``physical'' interpretation of this?
. Things change
substantially. Again, what is the ``physical'' interpretation of this?