MAT331 homework problems
NOTE:
Neither of these problems involve Maple, except as a word processor to
write your solution. If you like, you are welcome to turn in a printed
or handwritten version, if you are more comfortable with that.
- 11.
- (expires 2/25) Following Section 4 of the notes, prove
that if we describe the circle of center
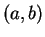 and radius
and radius 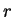 using
the parameters
using
the parameters 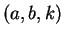 , with
, with
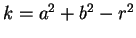 , rather than the
more natural parameters
, rather than the
more natural parameters 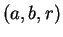 , then the error function
, then the error function
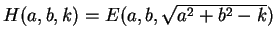 is quadratic in
is quadratic in 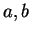 and
and 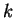 . What does
this imply about the number of critical points?
. What does
this imply about the number of critical points?
- 12.
- (expires 2/25) With reference to Problem #11, show that, for
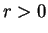 , the
transformation
, the
transformation
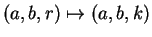 is a
valid change of variables, that is, it is one-to-one. This should help you
prove that
is a
valid change of variables, that is, it is one-to-one. This should help you
prove that 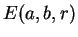 has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of
has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of 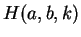 .
.
MAT 331
2002-02-18