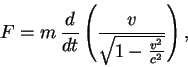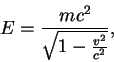- 7.
- (expires 2/18)
Fit the points
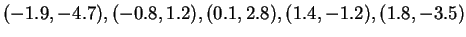 by means of a quadratic function
by means of a quadratic function
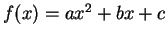 , using the least square method. First, do this
step by step, as we did in class; then, use the built-in Maple command,
described in the notes. Check that the two solutions agree.
, using the least square method. First, do this
step by step, as we did in class; then, use the built-in Maple command,
described in the notes. Check that the two solutions agree.
- 8.
- (expires 2/18)
Fit the set of points
with
a line, using the least square method we used in class. You will see
that this is not a good fit. Think of a better way to do the fit and
use Maple to do it. Explain in your solution why you think your better
way is better.
- 9.
- (expires 2/18)
In this problem we will estimate the charge of
the electron: If an electron of energy
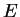 is thrown into a magnetic
field
is thrown into a magnetic
field 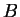 , perpendicular to its velocity, its trajectory will be
deflected into a circular trajectory of radius
, perpendicular to its velocity, its trajectory will be
deflected into a circular trajectory of radius 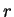 . The relation
between these three quantities is:
. The relation
between these three quantities is:
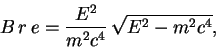 |
(1) |
where 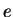 and
and 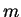 are, respectively, the charge and the mass of the
electron, and
are, respectively, the charge and the mass of the
electron, and 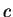 is the speed of light. The rest mass of the electron
is defined as
is the speed of light. The rest mass of the electron
is defined as 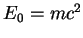 , and is about equal to
, and is about equal to
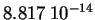 Joules. In our experimental set-up the energy of the emitted
electrons is set to be
Joules. In our experimental set-up the energy of the emitted
electrons is set to be 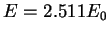 .
.
Use
read to make Maple load and execute the commands in the file
electron_data.txt, which is located in the
Worksheets directory of the
mat331 account.
This defines a list called
electron. Each element of the list is
a pair of the form ![$[B_i,r_i]$](img14.gif) , and these quantities are expressed in
Teslas and meters. Use least square fitting to determine the best value
for
, and these quantities are expressed in
Teslas and meters. Use least square fitting to determine the best value
for  . [Hint: Notice that the right hand side of (1) is
just a constant--calculate it once and for all and give it a name. Then
(1) is a very easy equation, which is linear in the unknown
parameter
. [Hint: Notice that the right hand side of (1) is
just a constant--calculate it once and for all and give it a name. Then
(1) is a very easy equation, which is linear in the unknown
parameter  . To verify your solution:
. To verify your solution:
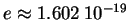 Coulomb].
Coulomb].
Physical constants courtesy of N.I.S.T.
- 10.
- (expires 2/18)
Prove relation (1), knowing the
following physical facts: In relativistic dynamics Newton's law is
replaced by
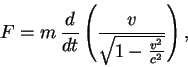 |
(2) |
where  is the force acting on a particle,
is the force acting on a particle,  its mass and
its mass and 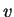 , a
function of time, its velocity. In the case at hand, the force exerted
by a magnetic field
, a
function of time, its velocity. In the case at hand, the force exerted
by a magnetic field 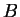 on an electron is
on an electron is
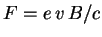 . Recall
that in a circular motion the acceleration
. Recall
that in a circular motion the acceleration
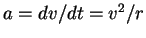 ,
, 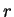 being the radius of the circle. Since (1) is expressed in
terms of the energy, rather than the velocity, you also need
Einstein's formula,
being the radius of the circle. Since (1) is expressed in
terms of the energy, rather than the velocity, you also need
Einstein's formula,
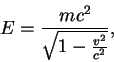 |
(3) |
which can be solved in terms of 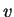 .
.
MAT 331
2002-02-10