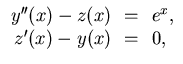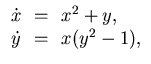MAT 331 Homework Exercises. Week 6 (Oct 28, 99).
- #21 (exp. 11/9)
- [No Maple] Find all the solutions to the differential
equation
Among them, single out the one for which x(0) = 3.
- #22 (exp. 11/9)
- Have Maple solve the following system of
differential equations,
with initial conditions:
y(0) = 1, y'(0) = 0, z(0) = k. Let us denote
the solutions by
yk(x), zk(x) (since they depend on the parameter
k). For k taking all integer values from -10 to 10, and
x
 [- 4, 2], plot on the same graph the functions yk, using a color,
and the functions zk, using a different color. [This is a
case when you don't want to retype the functions that Maple finds. See
prob. #06 for hints.]
[- 4, 2], plot on the same graph the functions yk, using a color,
and the functions zk, using a different color. [This is a
case when you don't want to retype the functions that Maple finds. See
prob. #06 for hints.]
- #23 (exp. 11/9)
- Find all the fixed points of the system
a fixed point being a solution for which both x(t) and y(t)
stay constant. For each of these points, describe the behavior of the
solutions that have initial conditions nearby.
- #24 (exp. 11/9)
- Consider the differential equation
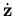 (t) = F(z(t)), where the vector
z(t) = (x(t), y(t)) and the field
F(x, y) = (- y, x - y). Plot a few
solutions. What happens to them when
t
(t) = F(z(t)), where the vector
z(t) = (x(t), y(t)) and the field
F(x, y) = (- y, x - y). Plot a few
solutions. What happens to them when
t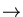 +
+ 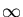 ?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
- #25 (exp. 11/9)
- [No Maple] For the equation
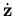 = F(z),
z = (x, y), with field
= F(z),
z = (x, y), with field
F(
x,
y) =
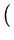
-
x(
x4 +
y4) -
y ,
x -
y(
x4 +
y4)
,
prove that the origin is an attractor in the future, i.e., every
solution verifies
[4]
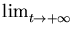 z(t) = 0. [Yes!
You can ask around how to do this, but then you have to show clearly
that you have understood it.]
z(t) = 0. [Yes!
You can ask around how to do this, but then you have to show clearly
that you have understood it.]
NOTE: The fact that we use various notations for
differential equations is purely intentional.
Translated from LaTeX by MAT 331
1999-10-28
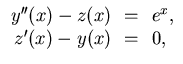
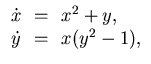
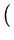 - x(x4 + y4) - y , x - y(x4 + y4)
- x(x4 + y4) - y , x - y(x4 + y4)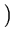 ,
,