Project 1: Plotting in 2 and 3 dimensions
Due Wednesday, 2 October
The goal of this project is to experiment with some graphics in maple.
To that end, we have several tasks to try, which vary in difficulty. You
may not be able to finish them all, but please do your best to attempt them
all. Where relevant, please include both the maple code to make the
figure, the figure itself, and any relevant text that describes what you are
doing. (this is more important in the later questions).
- Use maple to produce a good graph of the function
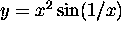 near the origin. You need to use some judgement about the precise
definition of the words ``good'' and ``near'', but the resulting graph
should be one that makes it clear that the function wiggles infinitely often
near 0, although the derivative at 0 exists (and is 0).
near the origin. You need to use some judgement about the precise
definition of the words ``good'' and ``near'', but the resulting graph
should be one that makes it clear that the function wiggles infinitely often
near 0, although the derivative at 0 exists (and is 0).
A slightly more difficult task is to produce a good graph of
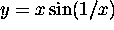 near 0. You might want to give this a try as well.
near 0. You might want to give this a try as well.
- Produce graphs of some spirals:
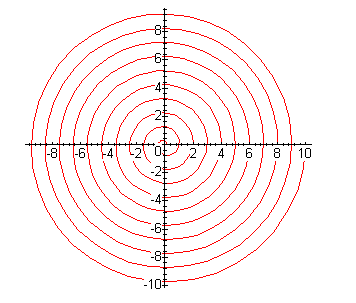
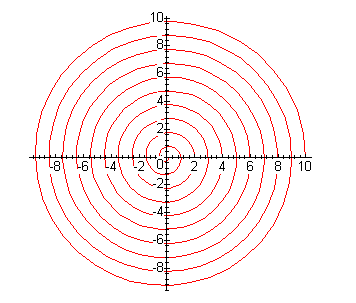
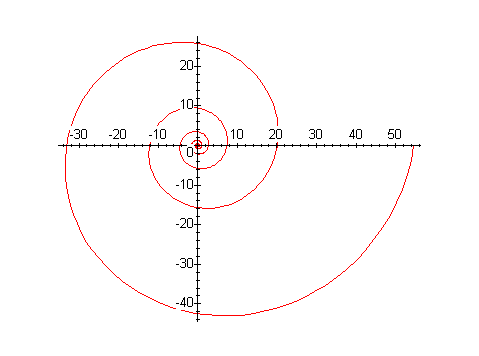

- a.
- A spiral which crosses the x-axis at all of the positive
integers, rotating clockwise.
- b.
- A spiral which crosses the x-axis at all of the positive
integers, rotating counter-clockwise.
- c.
- A logarithmic spiral. You may want to pay some
attention to the parameterization so that you get a nice, smooth
curve.
- d.
- Produce a ``Horn of Plenty'', that is, a
spiraling tube whose radius grows as it spirals out from the origin.
For fun, you might want to try to nest a few of these (see picture).
Or, since Thanksgiving is coming up, maybe fill it with pumpkins and
apples and other traditional foods.
- Produce a picture of a pair of rings linked together, and of the
``Borromean Rings''. For the latter, show a ``side view'' as well as the
standard view, so I can see how you twisted the rings through each other.
Can you make other nice knots or links, such as a trefoil knot?
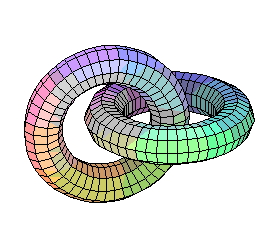
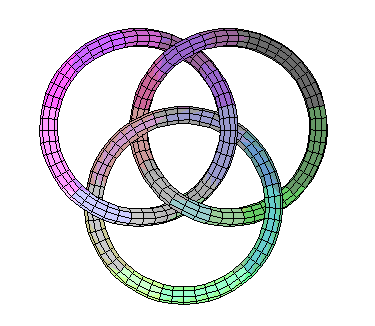
- Investigate the behavior of the parametric equations
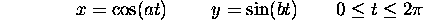
for various integer values of a and b. Can you make any conjectures
about what the pattern is? You might first try taking a=1 and letting b
vary from 1 to 5 or so. Then try it with a=2. (Yes, I know this question
is vague. I meant it to be so... just play around and make guesses,
then see if they work out.)
Scott Sutherland
Mon Sep 23 17:09:18 EDT 1996
![]() near 0. You might want to give this a try as well.
near 0. You might want to give this a try as well.



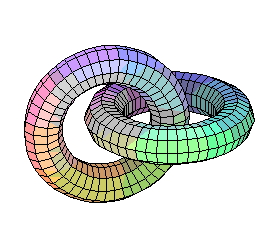
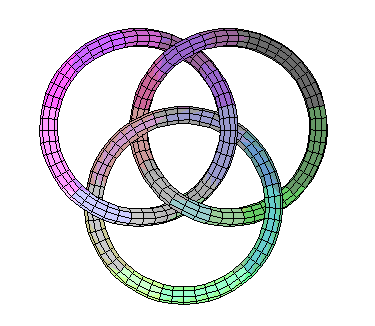
![]()