Math 331, Fall 2002: Problems 17-20
- 17.
- (expires 10/28)
Consider the differential equation
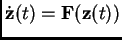 , where the vector
, where the vector
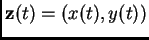 and the field
and the field
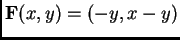 . Plot a few
solutions. What happens to them when
. Plot a few
solutions. What happens to them when 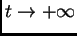 ?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
- 18.
- (expires 10/28) (No Maple.)
For the equation
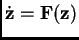 ,
,
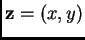 , with the vector field
, with the vector field
prove that the origin is an attractor in the future, i.e., every
solution verifies
[You can ask around how to do this, but then you have to show clearly
that you have understood it.]
- 19.
- (expires 10/28)
For the system of differential equations of
prob. #23,
find the eigenvalues and eigenvectors of the Jacobian at the fixed points.
[This is a give-away if you have done #16.]
- 20.
- (expires 10/28)
Consider the equations of the glider with no drag
term (
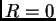 ). Use
dsolve, type=numeric to solve them numerically
with initial conditions
). Use
dsolve, type=numeric to solve them numerically
with initial conditions 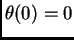 ,
, 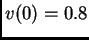 . Then solve exactly the
linearized system around the fixed point
. Then solve exactly the
linearized system around the fixed point
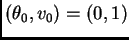 , with
the same initial conditions. Graph the two functions for
, with
the same initial conditions. Graph the two functions for 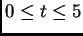 ,
and give a good estimate of their maximum difference. What happens if we
take a larger
,
and give a good estimate of their maximum difference. What happens if we
take a larger 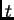 -range?
-range?
MAT 331
2002-10-21
