- 10 is a prime number.
- Are there any even prime numbers?
- Turn off that music or I'll scream.
- Life is good.
- 3+5.
- The number
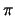 is bigger than 4.
is bigger than 4.
- Benjamin Franklin had many friends.
- The Chicago Cubs will win the World Series in the year 2106.
- I like olives but not very much.
- Goldbach's conjecture is true. (This was described in Chapter 1.)
-
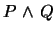 and
and
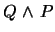
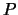 and
and
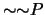
-
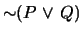 and
and
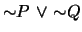
-
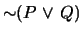 and
and
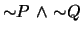
-
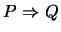 and
and
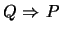
-
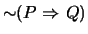 and
and
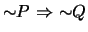
-
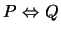 and
and
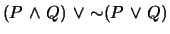
-
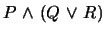 and
and
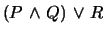
-
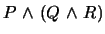 and
and
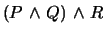
-
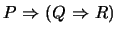 and
and
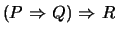
-
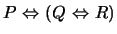 and
and
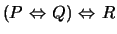
- Construct the truth table for
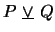 .
.
- Write a statement using our five basic connectives that is equivalent
to
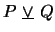 .
.
- Write a statement using only the connectives
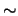 ,
, 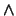 , and
, and
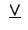 that
is equivalent to
that
is equivalent to
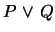 .
.
- Make up an English sentence in which you feel the word ``or'' should be interpreted inclusively.
- Make up an English sentence in which you feel the word ``or'' should be interpreted exclusively.
- Make up an English sentence in which you feel the word ``or'' can be interpreted either way.
- I need to go to Oxnard and Lompoc.
- If a number is even and bigger than 2, it's not prime.
- You're damned if you do and damned if you don't.
- If you order from the dinner menu, you get a soup or a salad, an entree, and a beverage or dessert. (Be careful with the word ``or'' in this one.)
- If it doesn't rain in the next week, we won't have vegetables or flowers, but if it does, we'll at least have flowers.
- No shoes, no shirt, no service. (Of course, this is a highly abbreviated sentence. You have to interpret it properly.)
- Men or women may apply for this job. (Be careful; this one's a bit tricky.)
- (a)
- If a symbolic statement has just one propositional variable (say
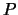 ),
how many lines are in its truth table?
),
how many lines are in its truth table?
- (b)
- How many different possible truth functions are there for such a statement? That is, in how many ways can the output column of such a truth table be filled in? Explain.
- *(c)
- Repeat parts (a) and (b) for a symbolic statement with two
propositional variables
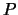 and
and 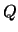 . Explain.
. Explain.
- *(d)
- On the basis of the previous parts of this problem, make
conjectures that generalize them to a symbolic statement with an arbitrary
number
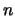 of propositional variables.
of propositional variables.