- If it rains, then either I will wear a coat or I'll stay home.
- This function has no inverse, and it is not continuous.
- In any triangle, the sum of the measure of the angles is less than
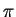 .
.
- For every
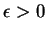 , there is a
, there is a 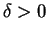 so that
so that
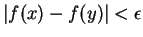 whenever
whenever
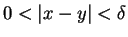 .
.
- Every natural number has a unique additive inverse.
As usual, we say
- For every integer
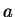 and every integer
and every integer 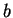 ,
, 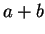 is positive and
is positive and
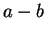 is negative.
is negative.
- There are integers
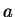 and
and 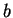 so that
so that 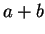 is positive and
is positive and 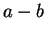 is
negative.
is
negative.
- For every integer
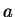 , there is an integer
, there is an integer 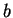 so that
so that 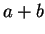 is
positive and
is
positive and 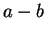 is negative.
is negative.
- There is an integer
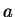 so that, for every integer
so that, for every integer 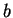 ,
, 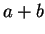 is
positive and
is
positive and 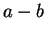 is negative.
is negative.
- m(x) means ``x is male''.
- f(x) means ``x is female''.
- P(x,y) means ``x is the parent of y''.
- (K1)
-
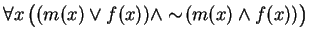
- (K2)
-
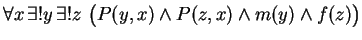
- State carefully, in common English, the meaning of axiom K1.
- State carefully, in common English, the meaning of axiom K2.
- Define the predicate
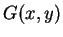 to mean
to mean
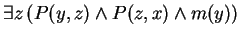 .
What is the common English meaning of
.
What is the common English meaning of 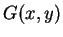 ?
?
- What is the meaning, in common English, of the assertion
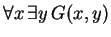 ?
?
- Prove that
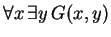 .
.