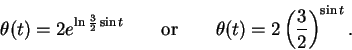Solution:
The linear function must be of the form
f(x) = ax+b. If f(0)=1,
then b=1. The fact that f(3)=3 gives us 3a + 1 =3, so a=2/3.
Thus, the linear equation is
f(x) = 2x/3 + 1.
An exponential function is of the form
g(x)= kecx. Since
g(0)=1, we have 1 = ke0, so k=1. Now using g(3) = 3 gives
us
![]() . Taking the logarithm of both sides yields
. Taking the logarithm of both sides yields
![]() . Thus
. Thus
![]() , giving
, giving
![]() . Notice that this reduces to
g(x)=3x/3.
. Notice that this reduces to
g(x)=3x/3.
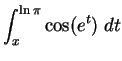
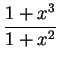
Solution:
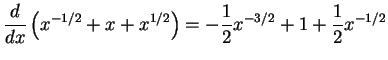
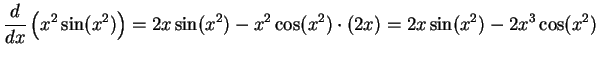 .
.
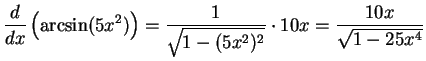
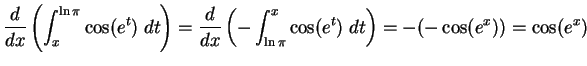 .
.
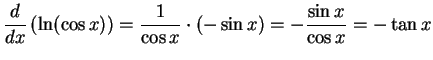 .
.
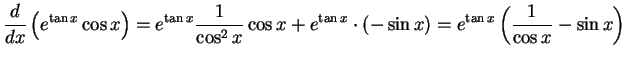 .
.
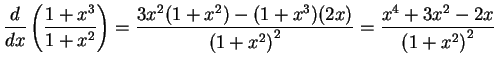 .
.
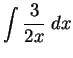
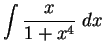
Solution:
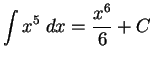 .
.
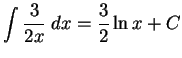 .
.
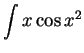 ,
first we notice that
because of the
,
first we notice that
because of the
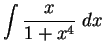 requires a bit of
thought. Rewriting it as
requires a bit of
thought. Rewriting it as
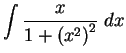 makes the answer more
apparent, however. If we guess that the antiderivative is
makes the answer more
apparent, however. If we guess that the antiderivative is
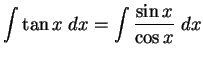 .
If we hadn't just seen this derivative in problem 1(f), this would be
harder. But we did, so the answer is obviously
.
If we hadn't just seen this derivative in problem 1(f), this would be
harder. But we did, so the answer is obviously
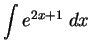 ,
we guess that
something like e2x+1 would work. Taking the derivative of that
shows that it is off by a factor of 2, so the correct antiderivative
must be
,
we guess that
something like e2x+1 would work. Taking the derivative of that
shows that it is off by a factor of 2, so the correct antiderivative
must be
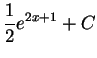
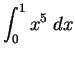
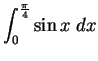
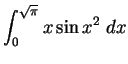
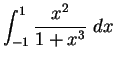
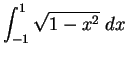
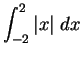
Solution:
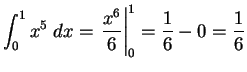 .
.
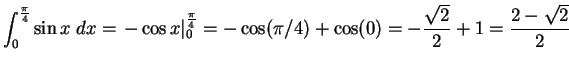 .
.
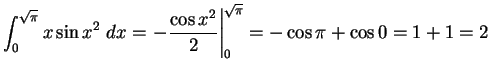 .
.
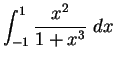 ,
first notice that the derivative of the bottom is 3x2, so
,
first notice that the derivative of the bottom is 3x2, so
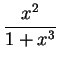 .
Thus, the value of the integral is
.
Thus, the value of the integral is
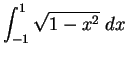 looks
really hard, unless you realize what it is the area of. This is the
area of the upper half of a circle of radius 1, so its value must be
looks
really hard, unless you realize what it is the area of. This is the
area of the upper half of a circle of radius 1, so its value must be
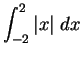 ,
we can either
realize this as the area of two triangles of base 2 and height 2or we can write it as
,
we can either
realize this as the area of two triangles of base 2 and height 2or we can write it as
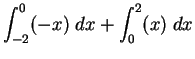 .
In either case, we get 2+2 = 4 as the result.
.
In either case, we get 2+2 = 4 as the result.
Solution:
The average value is given by
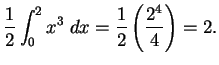
![]() that is
closest to the point (5,0). (Hint: if d is the distance from
(5,0) to a point on the curve, then it is permissible (and easier!)
to minimize d2.)
that is
closest to the point (5,0). (Hint: if d is the distance from
(5,0) to a point on the curve, then it is permissible (and easier!)
to minimize d2.)
Solution:
Let D(x) be the square of the distance from (5,0) to a point
![]() on the graph of
on the graph of
![]() . Then
. Then
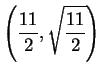 .
.
![]() ,
using n=4 rectangles. What should n be to ensure that the
right-hand sum is accurate to within 0.001? (Hint: compare the
expressions for the left-hand and right-hand sums for arbitrary n--
what does this tell you about the exact value of the integral?)
,
using n=4 rectangles. What should n be to ensure that the
right-hand sum is accurate to within 0.001? (Hint: compare the
expressions for the left-hand and right-hand sums for arbitrary n--
what does this tell you about the exact value of the integral?)
Solution:
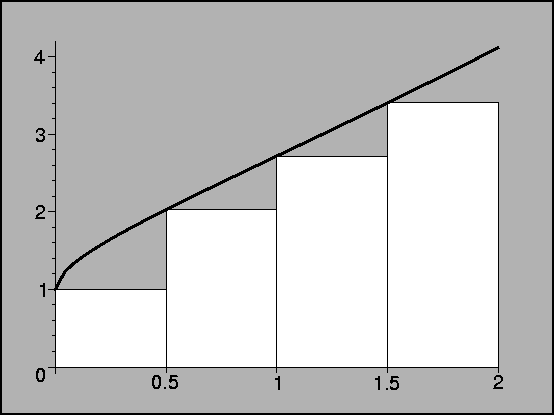
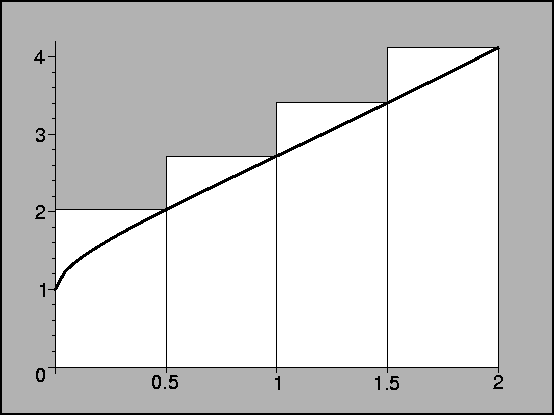
If we are using 4 rectangles, our points are x0=0, x1=1/2,
x2=1, x3=3/2, and x4=2. The left-hand sum is given by
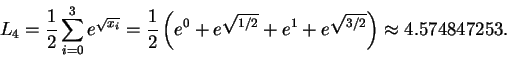
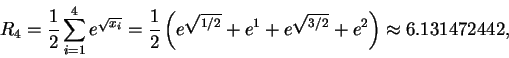
To determine what n should be to ensure that the left-sum has an
error of no more than 0.001, first notice that since
![]() is an increasing function, we always have
is an increasing function, we always have
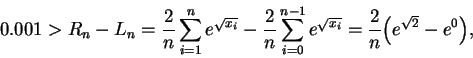
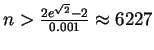 , we will be
guaranteed to have an answer that is within 0.001 of the value of
the integral. (In fact, using 3250 rectangles gives a left-sum that
is within 0.00096 of the correct answer.)
, we will be
guaranteed to have an answer that is within 0.001 of the value of
the integral. (In fact, using 3250 rectangles gives a left-sum that
is within 0.00096 of the correct answer.)
Solution:
The derivative of this function is
y' = 6x + 2, so at the desired point,
the slope is 6+2=8. The tangent line (also known as the first Taylor
polynomial) has the equation
Solution:
To find the slope at (1,1), we use implicit differentiation to obtain
3y2y' - 2(y + xy') + 3x2 = 0. At the point (1,1), this becomes
3y' -2 -2y' + 3 = 0, or y'=-1. Using this, we get a tangent line
of
Solution:
Let x represent the position of a point on the line from L1 to
L2, with L1 being at x=0 and L2 being at x=20. We need
to write an expression for the illumination at x, and find the value
of x which minimizes it. The illumination provided by L1 at xis given by 1/x2, and that provided by L2 is
8/(20-x)2, so
the total illumination at x is
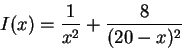
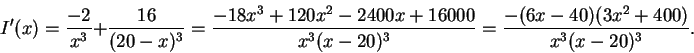
![]() .
.
Solution:
First we locate any critical points of the function by solving
f'(x)=0:
Solution:
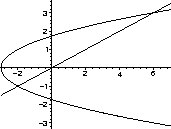
Notice that if you integrate with respect to x, things are harder--
the area is given by
![]() at
at
![]() (that is, the second Taylor polynomial). Use your
polynomial to find approximations of the nonzero solutions to
(that is, the second Taylor polynomial). Use your
polynomial to find approximations of the nonzero solutions to
![]() . (Hint: graph the relevant functions for
. (Hint: graph the relevant functions for
![]() to make sure your answers make sense. The
fact that
to make sure your answers make sense. The
fact that
![]() is helpful.)
is helpful.)
Solution:
Since
![]() and
and
![]() , the second Taylor
polynomial at
, the second Taylor
polynomial at ![]() is
is
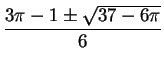 , or about 0.694 and
2.114. The solution we want is clearly 2.114, and because of
the symmetry, the other non-zero solution is near -2.114.
, or about 0.694 and
2.114. The solution we want is clearly 2.114, and because of
the symmetry, the other non-zero solution is near -2.114.
![]() to within 0.000005. You may either use your answer to the
previous problem as x0, or use x0=2.
to within 0.000005. You may either use your answer to the
previous problem as x0, or use x0=2.
Solution:
In this case, the Newton iteration is
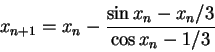
![]() ,
,
![]() , and ``does not exist''.
, and ``does not exist''.
Solution:
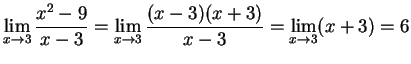
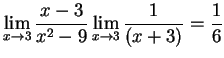
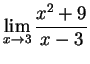 :
As
:
As 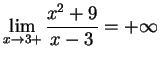 and
and
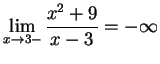 .
Hence the
two-sided limit does not exist.
.
Hence the
two-sided limit does not exist.
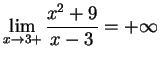 (see
part (d)).
(see
part (d)).
![]() .
.
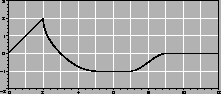
Solution:
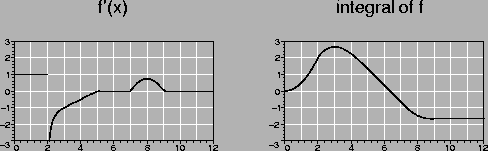
| (a) y'=5y | (1) y=x2 | |
| (b) y'=y(y-1) | (2) |
|
| (c) x2 y'' + 2x y' = 1 | (3) y=(1+e-x)-1 | |
| (d) yy'' = xy' | (4) y=e5x |
Solution:
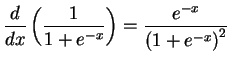 .
On the other side, we have
.
On the other side, we have
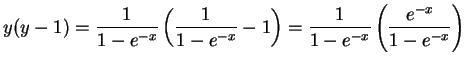 ,
so they are
the equal.
,
so they are
the equal.
![]() . When the depth is
. When the depth is ![]() , the
water level drops at a rate of
, the
water level drops at a rate of
![]() . What is the ratio of the
height of the cone to its radius? You may find it useful to recall that
the volume of a cone of radius r and height h is
. What is the ratio of the
height of the cone to its radius? You may find it useful to recall that
the volume of a cone of radius r and height h is
![]() .
.
Solution:
Let V(t) denote the volume of water in the cone at time t, and
h(t) be the depth of the water, with r(t) being the radius at
height h. Since the water is in a cone, the ratio r/h is always
constant; let us denote this constant by c, and it is 1/c we need
to determine.
We are told that water drains out at a rate of
![]() -- this
says that V'(t)=-10. Further, we know that when h(t)=8,
h'(t)=-2. Finally, the volume of water at any given time is
-- this
says that V'(t)=-10. Further, we know that when h(t)=8,
h'(t)=-2. Finally, the volume of water at any given time is
![]() .
.
Note that if we just differentiate the expression for the volume, we
will get something involving both r(t) and r'(t), but we don't
know anything about either of those. However, if we use that
r(t)/h(t)=c, we can rewrite the expression for V(t) not to involve
r(t) at all:
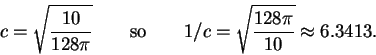
![]() be the parametric curve given by
be the parametric curve given by
Solution:
We want to compute
![]() at (4,2)-- remember that
at (4,2)-- remember that
![]() .
In our case,
.
In our case,

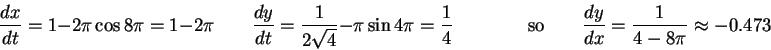
![]() is known to vary periodically with time, in such a
way that its rate of change is proportional to the product of itself
and the cosine of the time t. Write a differential equation which
expresses this relationship. Show that
is known to vary periodically with time, in such a
way that its rate of change is proportional to the product of itself
and the cosine of the time t. Write a differential equation which
expresses this relationship. Show that
![]() is a
solution to the differential equation. If you know that
is a
solution to the differential equation. If you know that
![]() and
and
![]() , what is the equation for
, what is the equation for ![]() ?
?
Solution:
This relationship can be written as
If we know
![]() , then we have
2 = ce0 = c. Using
, then we have
2 = ce0 = c. Using
![]() , we have
, we have
![]() . So
. So
![]() . Taking logarithms, we get
. Taking logarithms, we get
![]() . Thus
. Thus