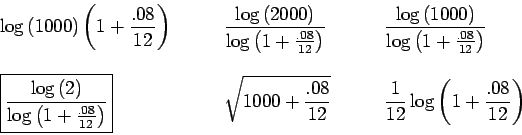
Solution:
Since we want to double our money, the future value should be $2000. As
above, the periodic rate is
![]() , the principle is $1000, and
the time is in months. Thus, we need to solve
, the principle is $1000, and
the time is in months. Thus, we need to solve
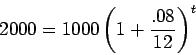
for
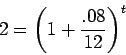
and then take the logarithm of both sides. Using the fact that
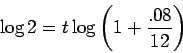
Now divide to get
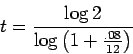
This is 104.31 months, that is, just over 8 years and 8 months.
(Note that this question is exactly the same as on quiz 3, problem 3, except this time the correct answer was one of the choices.)
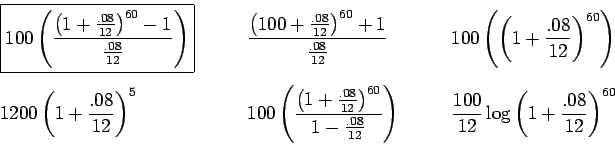
Solution:
This is exactly the formula for systematic savings, with the proper numbers
plugged in. More specifically, we make a deposit of $100 at the end of
each month, so there should be a 100 in front. Since the annual rate is 8%
and we are compounding monthly, the periodic rate is .08/12, and the time
should be in months. 5 years is 60 months, so we have
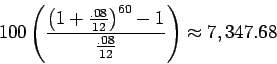
The amount we put into the account is $1,200 a year for 5 years, or $6,000. We make nearly $1,350 in interest.
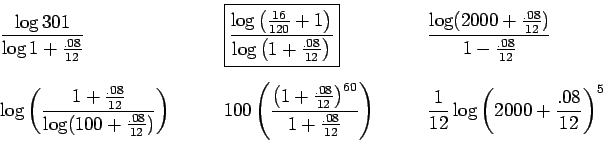
Solution: I think I must be cursed on the third problem of these quizzes. Yet again, there was a typo and the correct answer didn't appear. I've changed the answer above, and will give the correct solution here. Of course, everyone got full credit anyway.
Since we want to know the time to have $2000, we use the systematic savings
formula to get
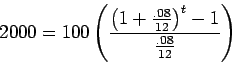
To solve this for
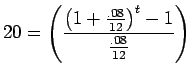 ,
and then multiply both sides by .08/12:
,
and then multiply both sides by .08/12:
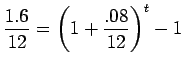
Now add 1 to both sides, and take the logarithm (I also rewrote
![]() as
as
![]() , more reduction is possible):
, more reduction is possible):
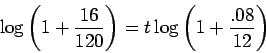
Solving for ![]() gives
gives
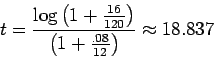
So, it will take 19 months to have more than $2000.