


Next: Converting (SP) to (SSP)
Up: Subset-Sum Problems and NP-Completeness
Previous: Subset-Sum Problems and NP-Completeness
Contents
We will use capitalletters  ,
, 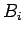 , to stand for logical variables. These
stand for statements like ``221 is a prime number'' or
``TH is the most common two-letter sequence in English,''
which are either true or false, i. e., these variables have
values of either T or F.
, to stand for logical variables. These
stand for statements like ``221 is a prime number'' or
``TH is the most common two-letter sequence in English,''
which are either true or false, i. e., these variables have
values of either T or F. 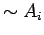 (``not
(``not  '') is the
statement that
'') is the
statement that  is false, so it has value T if
is false, so it has value T if  has
value F, and
has
value F, and 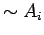 has value F if
has value F if  has value T.
We will also be interested in more elaborate formulas:
has value T.
We will also be interested in more elaborate formulas:
This formula says that either 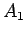 is true or
is true or 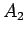 is false, or
is false, or
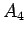 is false, etc. The value of this formula will be T unless
is false, etc. The value of this formula will be T unless
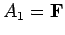 ,
, 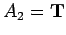 ,
, 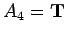 ,
, 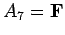 ,
, 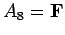 . Thus, there is only
one way in which the formula will be false.
. Thus, there is only
one way in which the formula will be false.
Figure 1 illustrates a satisfiability problem.
Figure 1:
A small (SP)
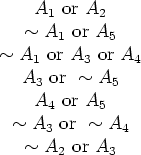 |
We want to assign T, F to all the variables so that
all of the formulas have value T. Even in this small example, it
may take you a minute or so to find such an assignment.



Next: Converting (SP) to (SSP)
Up: Subset-Sum Problems and NP-Completeness
Previous: Subset-Sum Problems and NP-Completeness
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14