next up previous contents
Next: Cook's Theorem Up: Subset-Sum Problems and NP-Completeness Previous: Converting (SP) to (SSP)

  
Converting (SSP) to (SP)

Suppose we have a subset-sum problem with 50 $a_i$, all between 1 and $2^{20}$, with $T<50(2^{20})<2^{26}$. Solving the SSP may be crudely broken into two steps:
1.
Decide which $a_i$ are in the subset.
2.
Verify that the sum of the chosen $a_i$ is $T$.
Our (SP) will also carry out these steps. The first is simple: we will have logic variables $A_1,\dots,A_{50}$ with $A_i={\bf T}$corresponding to $a_i$ being in the subset. To carry out the second step, we need to construct a set of logic formulas which acts as an ``adding machine'' to check the total.


We will represent numbers in base 2. Since all relevant numbers are $<2^{26}$, numbers may be represented by 26 logical variables. For each $1\le i\le50$, we will have variables $B_{i1},\dots,B_{i26}$. These will represent $a_i$ if $A_i={\bf T}$, 0 if $A_i={\bf F}$. To do this, we need formulas which show how the value of $A_i$ determines the value of all the $B_{ij}$:

\begin{displaymath}\sim A_i\hbox{ or }B_{ij}\quad A_i\hbox{ or }\sim B_{ij} \hbox{\quad if $j$th digit of $a_i=1$}\end{displaymath}

with the simple formula $\sim B_{ij}$if the $j$th digit of $a_i$ is 0.


Next, we need, for $2\le i\le 50$, variables $C_{i1},\dots C_{i26}$which represent the total of the first $i$ of the numbers given by the $B$-variables. Formulas are needed which show the $B$-variables deter mining the $C$-variables.


We begin with a set of formulas ${\cal S}(V,W,X,Y,Z)$ which have $Y$ get value T if and only if an odd number of $V,W,X$ have value T. $Z$ gets value T if and only if 2 or 3 of $V,W,X$ have value T:

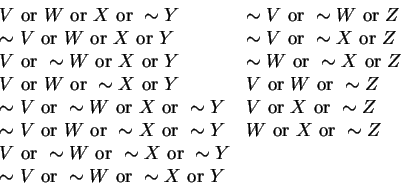
\begin{displaymath}\begin{array}{ll} V\hbox{ or }W\hbox{ or }X\hbox{ or }\sim Y ... ...sim V\hbox{ or }\sim W\hbox{ or }\sim X\hbox{ or }Y \end{array}\end{displaymath}

If $V,W,X$ represent three one-digit numbers (0 or 1), the formulas ${\cal S}(V,W,X,Y,Z)$ have the effect that $Y$ is the number in the column with the three numbers, while $Z$ shows whether there is a number carried into the next column.


We will use $D_{i1}$,...,$D_{i27}$, $2\le i\le 50$, to keep track of numbers being carried. Since there are no numbers carried in the rightmost column, we have the formulas $\sim D_{i1}$. The formulas

\begin{displaymath}{\cal S}(B_{1j},B_{2j},D_{2j},C_{2j},D_{2(j+1)})\qquad1\le j\le26\end{displaymath}

have the effect of making $C_{2j}$ represent the sum of the numbers $B_{1j}$and $B_{2j}$. To have $C_{ij}$represent the sum of $C_{(i-1)j}$ and $B_{ij}$, we use

\begin{displaymath}{\cal S}(B_{ij}, C_{(i-1)j}, D_{ij},C_{ij},D_{i(j+1)})\qquad 3\le i\le50\quad1\le j\le26\end{displaymath}


These logic formulas together have the effect that the $A_i$ determine the $B_i$, which determine $C_{2j}$ through $C_{50j}$ successively. This last group of variables corresponds to the base-2 representation of the sum of the $a_i$ which are in the set we have chosen. Finally, we add the formulas $C_{50j}$ or $\sim C_{50j}$ depending on whether the $j$th digit of $T$ is 1 or 0. As planned, a solution to this satisfiability problem gives a solution to the subset-sum problem (look at which $A_i$have value T), which implies that a method of solving (SP) can be used to solve (SSP).


The (SP) we have constructed is rather large, involving approximately $15(26)(50)$ formulas. However, the rate of growth if we had more $a_i$ with a larger upper limit is not too bad.

next up previous contents
Next: Cook's Theorem Up: Subset-Sum Problems and NP-Completeness Previous: Converting (SP) to (SSP)
Translated from LaTeX by Scott Sutherland
1998-03-15