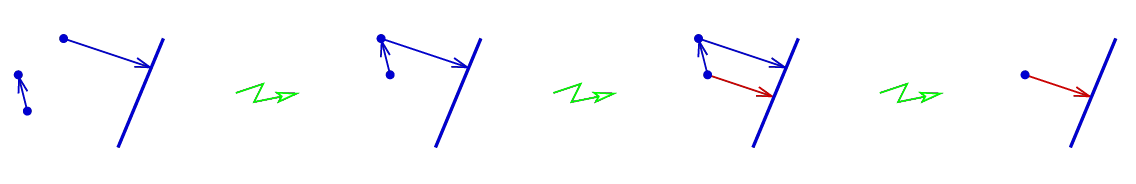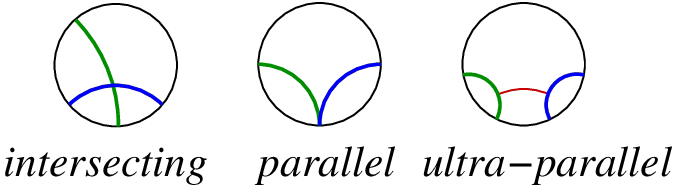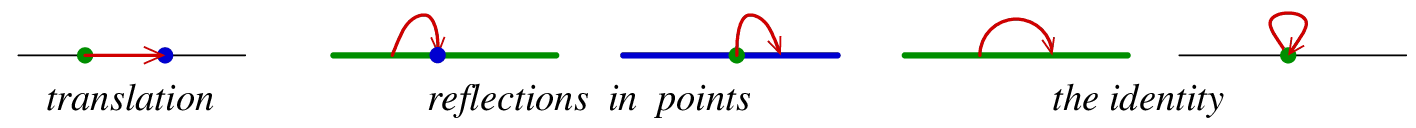Let $S$ and $T$ be isometries of the hyperbolic plane. In this section we
describe how to find a biflipper for $S\circ T$, given biflippers of $S$ and
$T$.
If $S$ and $T$ are rotations, then we act as in the case of two rotations in
$\mathbb{R}^{2}$. Connect the fixed points of $S$ and $T$ by a line $L$. It belongs
to both $\mathcal{P}(S)$ and $\mathcal{P}(T)$. By Theorem 8.A there
exist biflippers $\overrightarrow{AL}$ and $\overrightarrow{LB}$, which
encode $T$ and $S$, respectively. The biflipper $\overrightarrow{AB}$ encodes
$S\circ T$.
If $S$ or $T$ is a rotation and the other of them is not, then we act as in
the case of rotation and translation. Let, say, $S$ be a rotation.
Choose a line from the $\mathcal{P}(T)$, which passes through the center of
$S$ and hence belong to $\mathcal{P}(S)$. Then do the same as above.
Any other situation can be easily reduced to one of these two. Choose any
biflippers $\overrightarrow{AB}$ and $\overrightarrow{CD}$ representing $T$
and $S$. If $A$ is not a line, change both $A$ and $B$ to make $A$ a
line.
Consider the biflipper $\overrightarrow{BC}$ and the corresponding
isometry $U=F_{C}\circ F_{B}$. Lines of the pencil $\mathcal{P}(U)$ cover the
whole plane. Choose a point $Q\in A$ and a line $L\in\mathcal{P}(U)$ passing
through $Q$. By Theorem 8.A, there is a biflipper
$\overrightarrow{LM}$ which encodes $U$. So,
|
$S\circ T=F_{D}\circ F_{C}\circ F_{B}\circ F_{A}=F_{D}\circ U\circ F_{A}=F_{D}\circ F_{M}\circ F_{L}\circ F_{A}$ |
|
Since $L$ and $A$ intersect, either $L=A$ and then $S\circ T=F_{D}\circ F_{M}$
(and we are done), or $F_{L}\circ F_{A}$ is a rotation and we are in the
situation considered above.
However, in most cases this reduction to rotations is not needed
and there is a direct simpler construction. Consider those cases.
Let $S$ and $T$ be parallel motion. Then the pencils $\mathcal{P}(S)$
and $\mathcal{P}(T)$ intersect (a common line is connecting the points on
the absolute which are the centers of these pencils), and this line can be
made the head of one biflipper and the tail of the other one.
Let both $S$ and $T$ have invariant lines $L$ and $M$ (i.e., each of $S$
and $T$ is either a translation, or a glide reflection, or a reflection) and $L$, $M$ be non
parallel lines distinct from each other. Then either $L$ and $M$ intersect,
or they are ultra parallel. In the latter case the pencils $\mathcal{P}(S)$
and $\mathcal{P}(M)$ have a common line and it can be made the head of a
biflipper encoding $T$ and tail of the biflipper encoding $S$. In the former
case, an intersection point of $L$ and $M$ can be made the head of a
biflipper encoding $T$ and tail of the biflipper encoding $S$.
A hyperbolic pencil of lines orthogonal to line $L$ and parabolic pencil of
lines with central point $Q$ on the absolute which does not belong to (the
closure of) $L$ have a common line. This allows to achieve head to tail
biflippers in the cases when one of the isometries is a parallel motion and the
other one has invariant line not containing the center of the parabolic
pencil of the other one.
Thus, the only situations, in which there is no biflippers for $S$ and $T$ in
head to tail position, are when either both $S$ and $T$ have invariant lines
and these lines are parallel, or one of the isometries is parallel motion the
other has an invariant line and this line is parallel to the lines of the
pencil of lines of the parallel motion. These are degenerate situations
and for them one has to make a preliminary replacement of $S$ and $T$ which
would not affect $S\circ T$. The preliminary replacement can be done so
that $T$ would be replaced by a rotation, as it was described above.
⤶
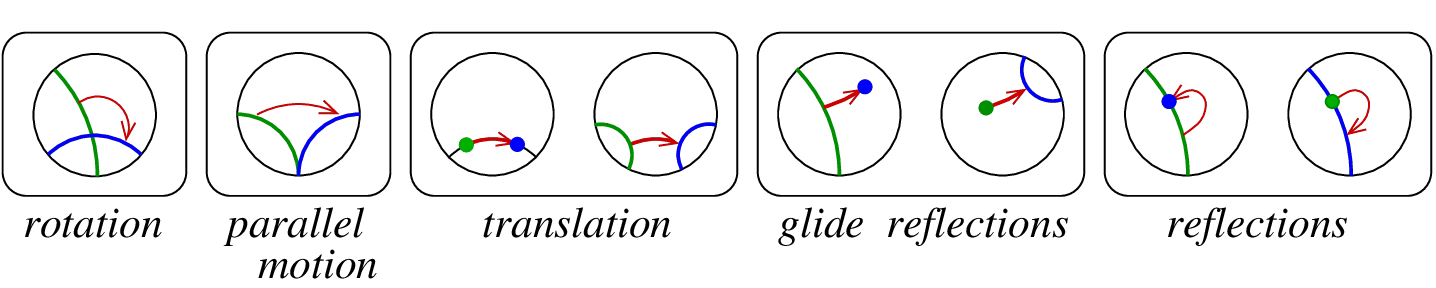
 and
and 
 and
and 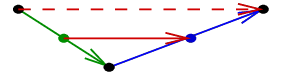
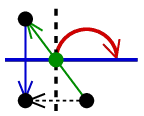
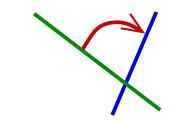 encodes the rotation about
the intersection
point of the flippers, in the direction from the tail flipper to the head
flipper,
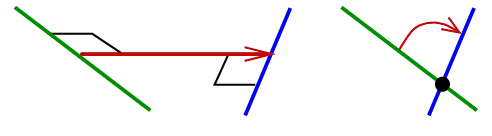
by the angle twice greater than the angle between them. A sketch of
proof:
encodes the rotation about
the intersection
point of the flippers, in the direction from the tail flipper to the head
flipper,
by the angle twice greater than the angle between them. A sketch of
proof: 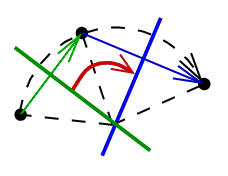
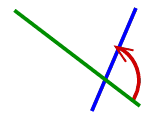

 and
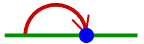
and  encode glide reflections.
This is the
reflection in the line which contains the arrow, followed by the translation
in the direction of the arrow by the distance twice greater than the length
of the arrow. Sketches of proofs:
encode glide reflections.
This is the
reflection in the line which contains the arrow, followed by the translation
in the direction of the arrow by the distance twice greater than the length
of the arrow. Sketches of proofs:
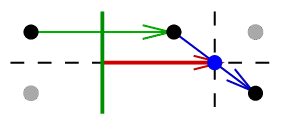 and
and
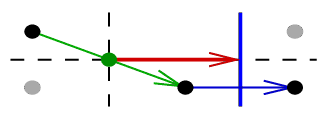
 and
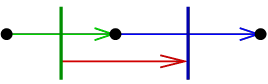
and 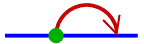 encode reflections;
specifically, the reflections in the line which is perpendicular
to the line-flipper, and erected from the point-flipper. Sketches of proofs:
encode reflections;
specifically, the reflections in the line which is perpendicular
to the line-flipper, and erected from the point-flipper. Sketches of proofs:
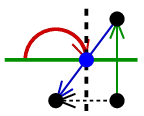 and
and