
Top
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6
(a
1) IF you used a basis

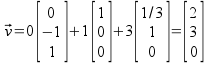
Alternative Method:
you will get the same answer by using Basis change matrix
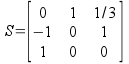
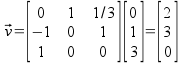
(

Solution 1-(b) Solution: You will solve the following equation for a,b,c
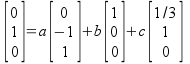
which amounts to solve
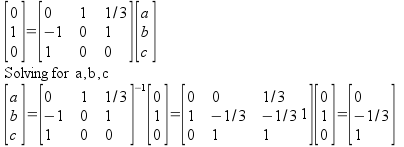
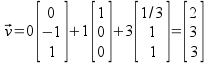
Alternative Method: You will get the same answer by using Basis change matrix
![]() =
=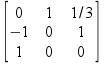
![]()
1-(b-)
If you are using
 as a basis
as a basis
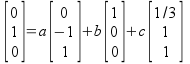
which amounts to solve
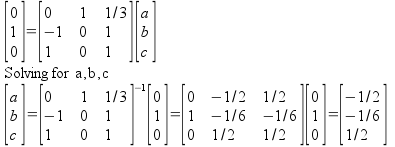



Top
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6
Solution: 2
(b) Nullity + Rank = Dimension of the domain = 3
(c)
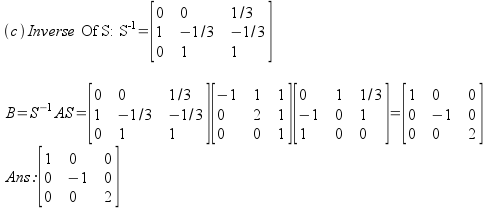
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6

![]()
![]()
![]()
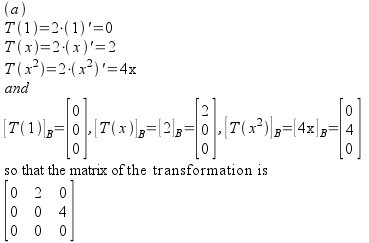
(b)To find the kernel we set
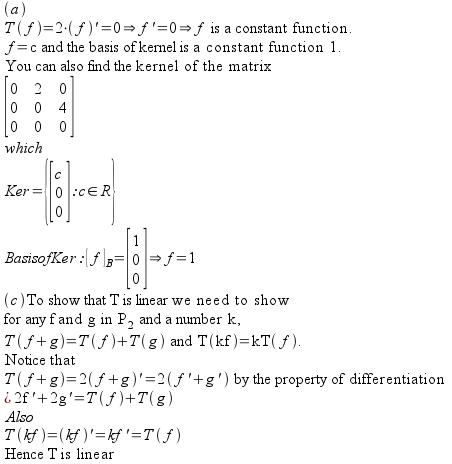
(d) But T is not an isomorphism because it is not 1-1 since Kernel has more than 0; .not only zero function but also all constant functions.
to
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6
Solution to Problem 4:
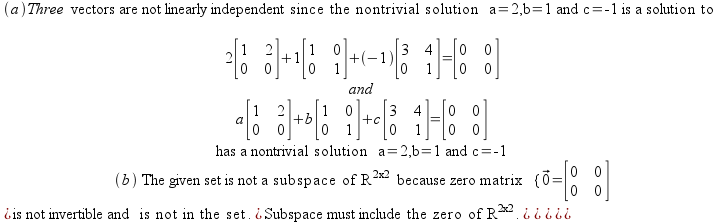
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6
Solution to Problem 5:
expand minor along any row or colum. I chose the row 1
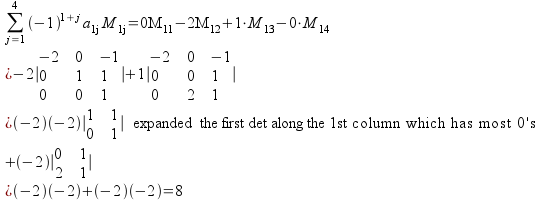
Ans: 6
Determinant of a triangular matrix is the product of the diagonals.
det = 2*1*3*1=6
Ans: 0
Notice that the first row and the 4th row are same. If we call the given matrix by A and rows by E1,E2, E3 and E4.
Subtract the 1st row from the last row gives the last row all 0.
the determinant of a matrix whose row is all zero is zero. (expand minors by the zero row. )
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6
Solution to 6. The determinant is a multilinear map with regards to column. I.e.
Start with a nxn square matrix with (n-1) columns fixed and one column is a variable.
T is a linear transformation on one column. at a time. Ie.
(b)
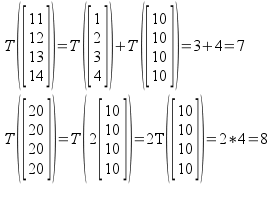
Solution to Problem 1 with changed basis
Solution to Problem 1 with unchanged basis
Solution to Problem 2
Solution to Problem 5
Solution to Problem 6