
Next: About this document ...
Sample Test: MA 3210, Midterm 1, Spring 2000
- 1.
- (1)Write the definition of mutually exclusive events.
(2) Adam knows that
P(A), P(E). Can you find
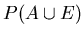 for him? What more information do you need to find it?
for him? What more information do you need to find it?
(3) What does it mean that two events A and B are independent? I.e. write down the definition of the independent events.
(4) Write down an example of independent events.
(5) What does it mean that three sets A, B, C form a partition of S.
(6) Adam knows
P(A|E), P(A) and P(E). Find
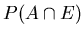 for him if he has enough information.
for him if he has enough information.
(7) Adam knows
P(A), P(B) and A, B are independent. Does he have enough information to find
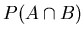 ? If so find it for him.
? If so find it for him.
(8) Adam knows P(A|E). Can you find
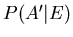 ?
?
(9) Adam knows that
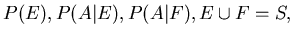 and
and
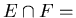 ,
does he have enough information to find P(E|A)? What more information does he need?
,
does he have enough information to find P(E|A)? What more information does he need?
- 2.
- The probability that OW students like mathematics is
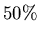 and the probability that OW students like history is
and the probability that OW students like history is 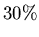 ,
and the probability that OW students like both mathematics and history is
,
and the probability that OW students like both mathematics and history is 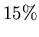 .
Find the probability that a randomly chosen OW student like mathematics or history,
probability that a randomly chosen OW student like mathematics but not history.
.
Find the probability that a randomly chosen OW student like mathematics or history,
probability that a randomly chosen OW student like mathematics but not history.
- 3.
- In the experiment of tossing a coin 5 times,
(1) how many different outcomes are possible?
(2) how many outcomes with 3 heads and 2 tails are possible?
(3) What is the probability that having 3 heads and 2 tails?
- 4.
- In a poker hand consisting of 5 cards, find the probability of holding
(1) 4 aces
(2) 3 spades and 2 club.
- 5.
- How many ways are there to distribute 1 motorcycle ,3 Honda Accords and 2 Mercedes to 6 winners, assuming everybody gets one.
- 6.
- How many permuations are possible to arrange the letters in "titanic"?
- 7.
- A coin is biased so that head is three times likely to occur as a tail. If a coin is tossed twice, what is the probability of getting 1 head and 1 tail?
- 8.
- In the above biased coin, if it is head one draws one ball from bag A and if it is a tail one draws a ball from the bag B.
Bag A contains 2 blue balls, 2 red balls and bag B contains 3 blue balls, 1 red ball.
(1) Complete the probability tree for this experiment.
(2)What is the probability
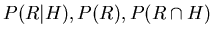 ,
where
,
where
R denotes the event of drawing a red ball, B denotes the event of drawing a blue ball and H and T denote the event of tossing a head and a tail respectively.
(3) Describe P(H|R) in words and find it.
- 9.
- Two fair dice are tossed. Adam is interested in finding the probability of sum of the two dice and Judy is interested in finding the largest number of the two dice.
(1) Find the probability that the sum is 10 for Adam.
(2) Find the probability that the sum is 8.
(3) Find the probability that the max number is 5 for Judy.
(4) Adam and Judy want to use the term random variable. He decided to use X for his random variable and she decided to denote her random variable as Z. Describe X.
(5) Find the outcomes (event) corresponding X=8 and find P(X=8)
(6) Find event whose random variable Z takes the value 4.
- 10.
- General Motor has 3 factories,
F1, F2, F3.
F1, F2, F3 make 20%, 45 %, and 35%, respectively of the products. The data shows that 3 %, 2% and 4 % of the products made by each factory are defective.
If one product is randomly selected,
(1) what is the probability that it is defective?
(2)What is the probability that a defective product is made by the Factory 1 F1?
Hint: For the second question, express the probability using the probability notation by completing the sentence that
Given the fact that the product is ( ),
what is the probability that the product is ( )?
In the real test, hint will not given to you.
- 11.
- A truth serum has the property that 80 % of the guilty suspects are properly judged while, of course, 20 % of guilty suspects are improperly found innocent. On the other hand, innocent suspects are misjudged 1 % of the time. If the suspect was selected from a group of suspects of which only 5 % have ever committed a crime, and the serum indicates that he is guilty, what is the probability that he is innocent?
- 12.
- Adam summarized to the following facts that
P(G | JG)=0.8, P(G |JI) = 0.01, P(I |G)=0.2, P( G)=0.05, where
G: A person is guilty
I: A person is innocent of the crime.
JI: Jury found the person innocent
JG: Jury found the person guilty.
(1) Describe the above 4 probabilities in words;
(2) Find the probability that the jury find the guilty. First fill in the blank below.
Given ( ),
the probability that ( ) is
what you want.
Now find the probability.
- 13.
- If (x, f(x)) is a probability function defined on the sample space with 4 outcomes a, b,c,d. Write down the 3 properties that f(x) has to satisfy. In other words, write the definition of a probability function in this setting of 4 outcomes.
- 14.
- Find the probability function for Andy's random variable X in ? and complete the probability histogram.
- 15.
- Find the cumulative distribution F(x) of the random variable X. Draw the graph of F(X).
- 16.
- (1) Show that f(x) is a probability density function
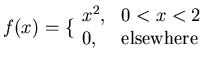
(2) Let F(x) denotes the cumulative distribution of f(x). Find F(1.5) and
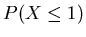 .
.


Next: About this document ...
Myong-Hi Kim
2001-09-27