The basic objects we study will be specific sets. For example, the sets of
integers, rationals, reals and complex numbers; denoted by
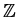 ,
,
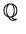 ,
,
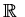 and
and
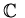 ,
respectively. The positive integers, rationals and reals are
denoted by
,
respectively. The positive integers, rationals and reals are
denoted by
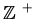 ,
,
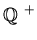 and
and
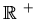 ;
the nonzero integers, rationals, reals
and complex numbers are denoted by
;
the nonzero integers, rationals, reals
and complex numbers are denoted by
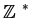 ,
,
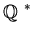 ,
,
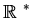 and
and
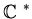 .
Most
of our sets will be built up from these objects and the empty set
(
.
Most
of our sets will be built up from these objects and the empty set
(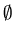 ). We will be using throughout the course the basic properties
of the fields of real and complex numbers.
). We will be using throughout the course the basic properties
of the fields of real and complex numbers.
Sets will usually be denoted by capital letters,
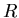 ,
,
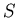 ,
...,
,
..., 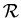 ,
,
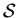 ,
...,
,
..., 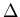 ,
,
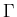 ,
... . Lower
case letters will usually denote elements of sets. The symbol
,
... . Lower
case letters will usually denote elements of sets. The symbol 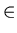 denotes
set membership; while the symbol
denotes
set membership; while the symbol 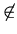 denotes ``not a member of.'' The
English sentences ``
denotes ``not a member of.'' The
English sentences ``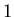 is an integer'' and ``
is an integer'' and ``
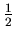 is not an
integer'' are written in symbols as ``
is not an
integer'' are written in symbols as ``
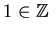 '' and ``
'' and ``
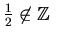 ''. Both statements are true. Whereas the statement ``
''. Both statements are true. Whereas the statement ``
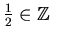 '' is not true. In the most common form of logic, the one we use, most
statements1 are either
true or not true. This does not imply that we can always
determine whether a given statement is true or not. Among other common
symbols we use are
'' is not true. In the most common form of logic, the one we use, most
statements1 are either
true or not true. This does not imply that we can always
determine whether a given statement is true or not. Among other common
symbols we use are 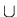 union,
union, 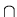 intersection,
intersection, 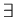 there
exists,
there
exists, 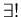 there exists a unique,
there exists a unique, 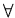 for all. We will often
describe sets by expressions like
for all. We will often
describe sets by expressions like
For example,
(the use of the semicolon ; in the
above expression is equivalent to the words such that - that will often be
abbreviated s.t.) and
The same set may be described in more than one way:
The formal definitions of 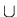 ,
set theoretic union,
and
,
set theoretic union,
and 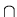 ,
set theoretic intersection, can
now be given as
,
set theoretic intersection, can
now be given as
and
Technically, the definition of 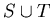 and the first of our two
definitions of
and the first of our two
definitions of 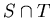 are not correct since they do not specify from
which set
are not correct since they do not specify from
which set 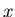 is chosen. All our operations must for technical foundational
issues be restricted to some universal set. In practical terms, this issue
seldom causes any problems for the topics that we will study. Two more
symbols that are commonly used involve set inclusion:
is chosen. All our operations must for technical foundational
issues be restricted to some universal set. In practical terms, this issue
seldom causes any problems for the topics that we will study. Two more
symbols that are commonly used involve set inclusion: 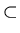 ,
,
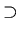 .
Both
.
Both
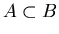 and
and
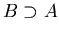 mean that every element of
mean that every element of
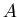 is in
is in 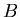 (
(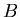 may coincide with
may coincide with 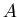 or be a ``bigger'' set than
or be a ``bigger'' set than
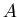 ). The inclusion
). The inclusion
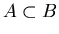 is proper if
is proper if 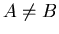 .
I2 will also us the symbol
.
I2 will also us the symbol 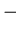 to denote
differences of sets3:
to denote
differences of sets3:
![]() ,
,
![]() ,
...,
,
..., ![]() ,
,
![]() ,
...,
,
..., ![]() ,
,
![]() ,
... . Lower
case letters will usually denote elements of sets. The symbol
,
... . Lower
case letters will usually denote elements of sets. The symbol ![]() denotes
set membership; while the symbol
denotes
set membership; while the symbol ![]() denotes ``not a member of.'' The
English sentences ``
denotes ``not a member of.'' The
English sentences ``![]() is an integer'' and ``
is an integer'' and ``
![]() is not an
integer'' are written in symbols as ``
is not an
integer'' are written in symbols as ``
![]() '' and ``
'' and ``
![]() ''. Both statements are true. Whereas the statement ``
''. Both statements are true. Whereas the statement ``
![]() '' is not true. In the most common form of logic, the one we use, most
statements1 are either
true or not true. This does not imply that we can always
determine whether a given statement is true or not. Among other common
symbols we use are
'' is not true. In the most common form of logic, the one we use, most
statements1 are either
true or not true. This does not imply that we can always
determine whether a given statement is true or not. Among other common
symbols we use are ![]() union,
union, ![]() intersection,
intersection, ![]() there
exists,
there
exists, ![]() there exists a unique,
there exists a unique, ![]() for all. We will often
describe sets by expressions like
for all. We will often
describe sets by expressions like