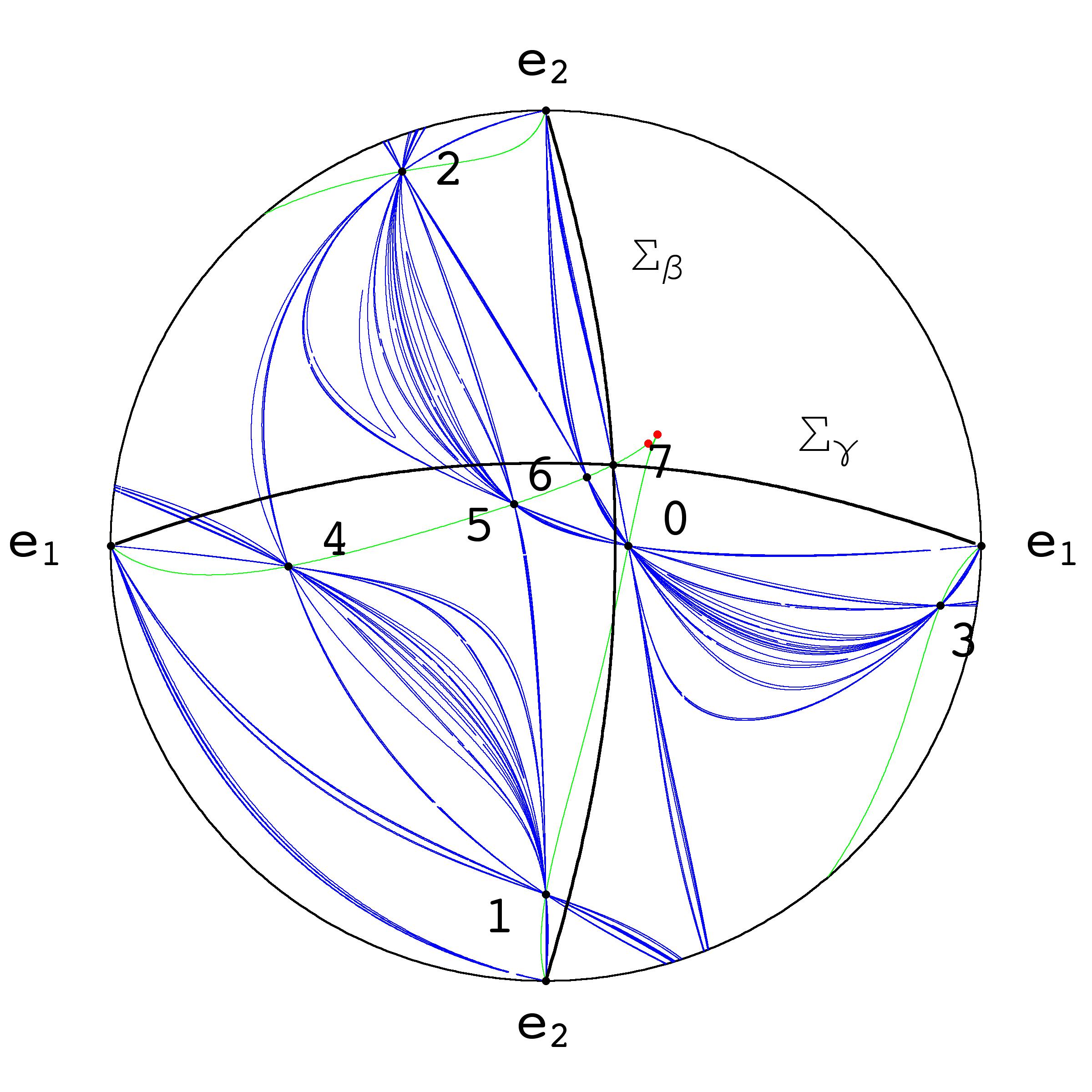

The disk pictured represents real projective space ${\Bbb R}{\Bbb P}^2$. The bounding circle is the line $\Sigma_0=\{x_0=0\}$. This is the real plane with with antipodal points identified: $[0:x_1:x_2]=[0:-x_1:-x_2]$. The disk also represents a compactification of ${\Bbb R}^2$: the polar ccoordinates $(r,\theta)$ are replaced by $(\rho,\theta)$, where $\rho=\arctan(\theta)$, so the disk pictured has radius $\pi/2$. $\Sigma_\beta$, $\Sigma_\gamma$ and $\Sigma_0$ are lines, but they appear to be curved in the $(\rho,\theta)$ coordinate system.
The map pictured is $$f_{a,b}(x,y)=(y,\frac{y+a}{x-b})$$ with $a=-.499497$, $b=-.415761$. This map is birational and has three exceptional lines, which are mapped to points: $\Sigma_\beta\mapsto e_2$, $\Sigma_0=\{x_0=0\}\mapsto e_1$, $\Sigma_\gamma \mapsto 0=(-a,0)$. The numbered points map '0'$\to$'1'$\to$'2'$\cdots\to$'7'$=\Sigma_\beta\cap\Sigma_\gamma$. The parameters $a$ and $b$ are algebraic numbers determined by the condition that $f_{a,b}^7$ maps the point '0'$=(-a,0)$ to the point '7'$=(-b,-a)$.
The green curve is an invariant cubic, and the two red dots are fixed points. The dot that appears to touch the number `7' is a saddle point, and the dot that is at the cusp point of the green curve is a repelling fixed point.
This map $f_{a,b}$ can be considered equally well as a map on ${\Bbb R}{\Bbb P}^2$ or on ${\Bbb C}{\Bbb P}^2$. We denote these two maps by $f_{\Bbb R}$ and $f_{\Bbb C}$. Let us consider the complex manifold $\pi:X\to {\Bbb C}{\Bbb P}^2$ obtained by blowing up the points $e_1$, $e_2$, '0', $\dots$ , '7', and let $X_{\Bbb R}$ denote the set of real points. If we lift $f_{a,b}$ to the map $f_X:=\pi^{-1}\circ f_{a,b}\circ \pi$, the we obtain an automorphism of $X$. A basic result is that if $L$ represents any complex line, then the normalized currents of integration over the iterates $\delta^{-n}[f^n(L)]$ converge to an invariant current $T^u$ as $n\to\infty$. This current has a laminar structure. The blue curve picture at right shows the 10th iterate of a line, and this seems to show some laminarity. The crossings of the blue curves at the points '$j$', $0\le j\le 7$ are artificats of the projection $\pi$: these curves will be disjoint in the space $X$. Does the real map $f_{\Bbb R}$ have an invariant current with laminar structure? If so, is this laminar current somehow obtained as the intersection of $T^u$ with $X_{\Bbb R}$?
It is known that $f$ is a real map of maximal entropy in the sense that $f_{\Bbb R}$ and $f_{\Bbb C}$ have the same entropy. In the case of Henon maps, when the real and complex maps have the same entropy, they have been shown to be quasi-hyperbolic. Is the present map $f_{a,b}$ also quasi-hyperbolic? Or is $f_{\Bbb R}$ possibly uniformly hyperbolic?