Completing the Square

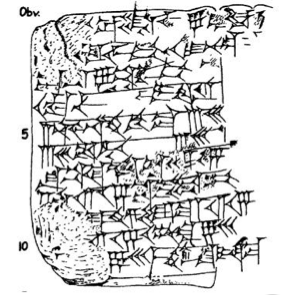
The Yale Babylonian Collection's tablet YBC 6967, as transcribed in in Neugebauer and Sachs, Mathematical Cuneiform Texts, American Oriental Society, New Haven, 1986. Size 4.5 $\times$ 6.5cm.

The Old Babylonian tablet YBC 6967 (about 1900 BC) contains a problem and its solution. Here is a line-by-line literal translation from Jöran Friberg, A Remarkable Collection of Babylonian Mathematical Texts, Springer, New York, 2007.

• The igi.bi over the igi 7 is beyond.
  The igi and the igi.bi are what?
  You:
  7 the the igi.bi over the igi is beyond
  to two break, then 3 30.
  3 30 with 3 30 let them eat each other, then 12 15
  To 12 15 that came up for you
  1, the field, add, then 1 12 15.
  The equalside of 1 12 15 is what? 8 30.
  8 30 and 8 30, its equal, lay down, then
  3 30, the holder,
  from one tear out,
  to one add.
  one is 12, the second 5.
  12 is the igi.bi, 5 the igi.

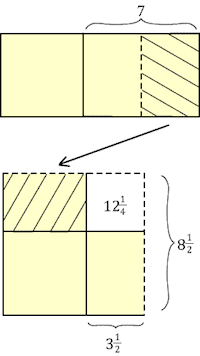
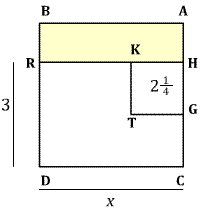
Diagram of solution of the YBC 6967 problem, adapted from Eleanor Robson's "Words and Pictures: New Light on Plimpton 322" (MAA Monthly, February 2002, 105-120). Robson uses a semi-colon to separate the whole and the fractional part of a number, but this is a modern insertion for our convenience. The two unknown reciprocals are conceptualized as the sides of a rectangle of area (yellow) 1 0 [or 60 in decimal notation]. A rectangle with one side 3;30 [$= 3\frac{1}{2}$] is moved from the side of the figure to the top, creating an L-shaped figure of area 1 0 which can be completed to a square by adding a small square of area 3;30 $\times$ 3;30 = 12;15 [$= 12\frac{1}{4}$]. The area of the large square is 1 0 + 12;15 = 1 12;15 [$ = 72\frac{1}{4}$] with square root 8;30 [$=8\frac{1}{2}$]. It follows that our unknown reciprocals must be 8;30 + 3;30 = 12 and 8;30 − 3;30 = 5 respectively.

In modern notation, the YBC 6967 problem would be $xy = 60, x-y = 7$, or $x^2-7x-60=0$. In this case the term to be added in completing the square is $\frac{b^2}{4a^2}=\frac{49}{4}=12\frac{1}{4}$, corresponding exactly to the area of the small square in the diagram.

This tablet, and the several related ones from the same period that exist in various collections (they are cataloged in Friberg's book mentioned above), are significant because they hold a piece of real mathematics: a calculation that goes well beyond tallying to a creative attack on a problem. It should also be noted that none of these tablets contains a figure, even though Old Babylonian tablets often have diagrams. It is as if those mathematicians thought of "breaking," "laying down" and "tearing out" as purely abstract operations on quantities, despite the geometrical/physical language and the clear (to us) geometrical conceptualization.

The Old Babylonian tablet Plimpton 322 (approx. $13 \times 9$ cm) is in the Columbia University Library. Image courtesy of Bill Casselman (larger image). For scholarly discussions of its content see Friberg's book or (available online) Eleanor Robson's article referenced above.

There have been many attempts at understanding why Plimpton 322 was made and also how that particular set of numbers was generated. It has been described as a list of Pythagorean triples and as an exact sexagesimal trigonometry table. An interpretation mentioned by R. Creighton Buck and attributed to D. L. Voils (in a paper that was never published) is "that the Plimpton tablet has nothing to do with Pythagorean triplets or trigonometry but, instead, is a pedagogical tool intended to help a mathematics teacher of the period make up a large number of igi-igibi quadratic equation exercises having known solutions and intermediate solution steps that are easily checked" (igi, igi.bi problems involve a number and its reciprocal; the one on YBC 6769 is exactly of this type).

In the solution of the problem of YBC 6769, we squared 3;30 to get 12;15, added 1 to get $1\, 12;15$ and took the square root to get 8;30. Then the solutions were 8;30 + 3;30 and 8;30 $-$ 3;30. So to set up an igi, igi.bi problem which will work out evenly we need a square like 12;15 which, when a 1 is placed in the next base-60 place to the left, becomes another square.

Now the first column of Plimpton 322 contains exactly numbers of this type. For example, in row 5, the first undamaged row, the column I entry is $48\, 54\, 01\, 40$ [=10562500] with square root $54\, 10$ [=3250]. Adding 1 gives $1\, 48\, 54\, 01\, 40$ [=23522500] with square root $80\, 50$ [=4850].
   The corresponding igi, igi.bi problem would ask for two reciprocals differing by two times $54\, 10$, i.e. $1\, 48\, 20$; the answer would be $80\, 50 + 54\, 10 = 2\, 15\, 00$ and $80\, 50 - 54\, 10 = 26\, 40$.

Unfortunately, neither the problem on YBC 6967 nor any of the five igi, igi.bi problems recorded by Friberg from tablet MS 3971 correspond to parameters on Plimpton 322. It is possible that lines on the bottom and reverse of the tablet mean that it was supposed to be extended to additional 20 or so rows, where those missing parameters would appear. In fact, none of the proposed explanations is completely satisfactory. As Robson remarked, "The Mystery of the Cuneiform Tablet has not yet been fully solved."

1. "roots and squares are equal to numbers" [$x^2 + bx = a$]
2. "squares and numbers are equal to roots" [$x^2 +a = bx$]
3. "roots and numbers are equal to squares" [$x^2=bx+a$]

Case 1. al-Khwarizmi works out a specific numerical example, which can serve as a template for any other equation of this form: "what must be the square which, when increased by ten of its roots, amounts to thirty-nine."

• "The solution is this: you halve the number of the roots, which in the present case equals five. This you multiply by itself; the product is twenty-five. Add this to thirty-nine, the sum is sixty-four. Now take the root of this, which is eight, and subtract from it half the number of the roots, which is five; the remainder is three. This is the root of the square which you sought for; the square itself is nine."

Note that this is exactly the Old Babylonian recipe, updated from $x(x+7)=60$ to $x^2 +10x = 39$, and that the figure Eleanor Robson uses for her explanation is essentially identical to the one al-Khwarizmi gives for his second demonstration, reproduced here:

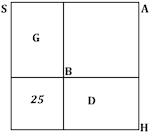
"We proceed from the quadrate AB, which represents the square. It is our next business to add to it the ten roots of the same. We halve for this purpose the ten, so it becomes five, and construct two quadrangles on two sides of the quadrate AB, namely, G and D, the length of each of them being five, as the moiety of the ten roots, whilst the breadth of each is equal to a side of the quadrate AB. Then a quadrate remains opposite the corner of the quadrate AB. This is equal to five multiplied by five: this five being half of the number of roots which we have added to each side of the first quadrate. Thus we know that the first quadrate, which is the square, and the two quadrangles on its sides, which are the ten roots, make together thirty-nine. In order to complete the great quadrate, there wants only a square of five multiplied by five, or twenty-five. This we add to the thirty-nine, in order to complete the great square SH. The sum is sixty-four. We extract its root, eight, which is one of the sides of the great quadrangle. By subtracting from this the same quantity which we have before added, namely five, we obtain three as the remainder. This is the side of the quadrangle AB, which represents the square; it is the root of this square, and the square itself is nine."

Case 2. "for instance, 'a square and twenty-one in numbers are equal to ten roots of the same square."

• Solution: Halve the number of the roots; the moiety is five. Multiply this by itself; the product is twenty-five. Subtract from this the twenty-one which are connected with the square; the remainder is four. Extract its root; it is two. Subtract this from the moiety of the roots, which is five; the remainder is three. This is the root of the square you required, and the square is nine.

Here is summary of al-Khwarizmi's demonstration. The last of the four figures appears (minus the modern embellishments) in Rosen, p. 18.

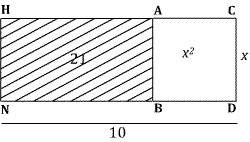
The problem set up geometrically. I have labeled the unknown root $x$ for modern convenience. The square ABCD has area $x^2$, the rectangle CHND has area $10x$, the rectangle AHNB has area 21, so $x^2+21=10x$.

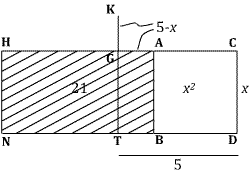
The side CH is divided in half at G, so the segment AG measures $5-x$. The segment TG parallel to DC is extended by GK with length also $5-x$. Al-Khwarizmi says this is done "in order to complete the square."

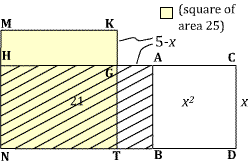
The segment TK then measures 5, so the figure KMNT, obtained by drawing KM parallel to GH and adding MH, is a square with area 25.

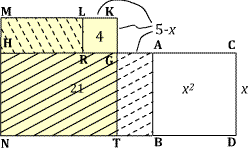
Measuring off KL equal to KG, and drawing LR parallel to KG leads to a square KLRG. Since HR has length $5-(5-x)=x$ the rectangles LMHR and AGTB have the same area, so the area of the region formed by adding LMHR to GHNT is the same as that of the rectangle formed by adding AGTB to GHNT, i.e. 21. And since that region together with the square KLRG makes up the square KMNT of area 25, it follows that the area of KLRG is $25-21=4$, and that its side-length $5-x$ is equal to 2. Hence $x=3$, and the sought-for square is 9.

Case 3. Example: "Three roots and four simple numbers are equal to a square."

• Solution: "Halve the roots; the moiety is one and a half. Multiply this by itself; the product is two and a quarter. Add this to the four; the sum is six and a quarter. Extract its root; it is two and a half. Add this to the moiety of the roots, which was one and a half; the sum is four. This is the root of the square, and the square is sixteen."

As above, we summarize al-Khwarizmi's demonstration. The last figure minus decoration appears on Rosen, p. 20.

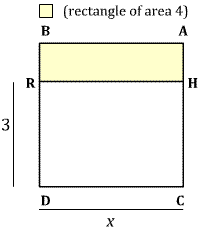
We represent the unknown square as ABDC, with side-length $x$. We cut off the rectangle HRDC with side-lengths 3 and $x$. Since $x^2 = 3x + 4$ the remaining rectangle ABRH has area 4.

Halve the side HC at the point G, and construct the square HKTG. Since HG has length $1\frac{1}{2}$, the square HKTG has area $2\frac{1}{4}$.

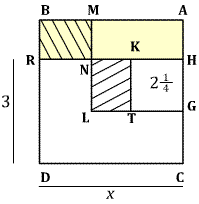
Extend CT by a segment TL equal to AH. Then the segments GL and AG have the same length, so drawing LM parallel to AG gives a square AGLM. Now TL = AH = MN and NL = HG = GC = BM, so the rectangles MBRN and KNLT have equal area, and so the region formed by AMNH and KNLT has the same area as ABRH, namely 4. It follows that the square AMLG has area $4+2\frac{1}{4}=6\frac{1}{4}$ and consequently side-length AG = $2\frac{1}{2}$. Since GC = $1\frac{1}{2}$, it follows that $x = 2\frac{1}{2} + 1\frac{1}{2} = 4$.

• 

  "The quadratic: the absolute quantities multiplied by four times the coefficient of the square of the unknown are increased by the square of the coefficient of the middle (i.e. unknown); the square-root of the result being diminished by the coefficient of the middle and divided by twice the coefficient of the square of the unknown, is (the value of) the middle."

The third section of chapter 15 of the Liber Abaci, written by Fibonacci (Leonardo of Pisa, c. 1170-c. 1245) in 1202, concerns "Problems of Algebra and Almuchabala," referring directly to the Arabic words for "Completion and Reduction" in the title of al-Khwarizmi's compendium. I am using the translation of Liber Abaci by L. E. Sigler, Springer, 2002. In that section, a short introduction presenting the methods is followed by a collection of over a hundred problems.
    Fibonacci follows al-Khwarizmi in distinguishing three "modes" of compound problems involving a square ("census") and its roots (his second mode corresponds to al_Khwarizmi's case 3 and vice-versa).

• "the first mode is when census plus roots are equal to a number." The example Fibonacci gives, "the census plus ten roots is equal to 39" is inherited directly from al Khwarizmi. But the demonstration he gives is different: he starts with a square $abcd$ of side length greater than 5, marks off lengths of 5 in two directions from one corner and thus partitions $abcd$ into a square of area 25, two rectangles and another square, which he identifies with the unknown census. Then the two rectangles add up to 10 times the root, but since "the census plus 10 roots is equal to 39 denari" the area of $abcd$ must be $25+39=64$, so its side length is 8, our root is $8-5=3$ and the census is 9. The figure and the calculation are essentially the same as al-Khwarizmi's, but the "completion" narrative has disappeared.

• "let the census be equal to 10 roots plus 39 denari." Here the example is new.
  

  (Figure from Sigler, p. 557). Fibonacci starts by representing the census as a square $abcd$ of side length larger than 10. He draws a segment $fe$ parallel to $ab$ so that the segments $fd$ and $ec$ each have length 10 and assigns a midpoint $g$ to $ec$. So the ten roots will be equal to the area of $fecd$, and the area of the rectangle $abfe$, which is also $fe\times eb$, is 39. But $fe=bc$, therefore $be \times bc = 39$. "If to this is added the square of the line segment $eg$, then 64 results for the square of the line segment $bg$." [$bg^2 = be^2 + 2be\times eg +eg^2$ $= be\times(be + 2eg)+ eg^2 = be\times(be+eg+gc)+eg^2$ $= be\times bc +eg^2 = 39+25=64$]. So $bg = 8$ and $bc = bg+gc = 8+5=13$ is the root of the sought census, and the census is 169.
  

• "when it will occur that the census plus a number will equal a number of roots, then you know that you can operate whenever the number is equal to or less than the square of half the number of roots." Here Fibonacci goes beyond al-Khwarizmi in remarking that (in modern notation) $x^2+c=bx$ has no solution if $c>(b/2)^2$. The example he gives is "let the census plus 40 equal 14 roots."
  

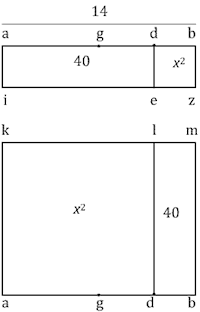
  (Figures from Sigler, pp. 557, 558). Fibonacci gives two construction for the two positive roots. In each case he starts with a segment $ab$ of length 14, with center at $g$. He chooses another point $d$ dividing $ab$ into two unequal parts.
      For the first root he constructs a square $dbez$ over $db$ --this will be the census-- and extends $ez$ to $iz$ matching $ab$. The rectangle $abzi$ now represents 14 roots, so that $adei$ measures (in modern notation) $14x - x^2 = 40$. Now $dg = 7-x$ so $dg^2 = 49-14x+x^2$ and $dg^2 + 40 = 49$. It follows that $dg=3$ and the root $x$ is $db=gb-gd=7-3=4$.
      For the second root the square $adlk$ is over $ad$; the segment $kl$ is extended to $km$ matching $ab$, and $lmbd$ measures $14x - x^2 = 40$. Now $gd = x-7$ so again $gd^2 = x^2-14x+49 = 9$ and $gd=3$. This time the root is $x=ag+gd = 10$.
  

Stevin's L'Arithmétique was published in 1594 (excerpts here are from the 1625 edition, supervised by Albert Girard). Among other things it treated quadratic equations. Stevin, following Bombelli, used a notation for powers that turns out to be intermediate between cossic notation (which used different symbols for the unknown, its square, its cube etc.) and the exponents that started with Descartes. For Stevin, the unknown was represented by a 1 in a circle, its square by a 2 in a circle, etc., and the numerical unit by a 0 in a circle. Here let us write ${\bf 1}$ for 1 in a circle, etc. He also had an idiosyncratic way of expressing the solution to an equation in one unknown, using the "fourth proportional." For example, his setting of the problem the problem of finding $x$ such that $x^2=4x+12$ could be schematized as $${\bf 2} : 4\,{\bf 1} + 12\,{\bf 0} : : {\bf 1} : ?$$ (he would actually write: given the three terms for the problem -- the first ${\bf 2}$, the second $4\,{\bf 1} + 12\,{\bf 0}$, the third ${\bf 1}$, find the fourth proportional). As Girard explains, the "proportion" is equality. So the problem should be read as: "if ${\bf 2} = 4\,{\bf 1} + 12\,{\bf 0}$, then ${\bf 1} =$ what?"

One can read "[Stevin's Arithmetic] brought to the western world for the first time a general solution of the quadratic equation ..." but in fact there is only this step towards modern notation, his use of minus signs in his equations and his admission of irrational numbers as coefficients to separate him from Fibonacci. Notably he also considers separately three types of quadratic equations [his examples, in post-Descartes notation]

1. "second term ${\bf 1} + {\bf 0}$" [$x^2=4x+12$]
2. "second term $-{\bf 1} + {\bf 0}$" [$x^2 = -6x + 16$]
3. "second term ${\bf 1} - {\bf 0}$" [$x^2=6x-5$].

Stevin gives a geometric justification for his solution of each type of equation. For example for the first type his solution is:

• Half of the 4 (from the $4\,{\bf 1}$) is	2
  Its square	4
  To the same added the given ${\bf 0}$, which is	12
  Gives the sum	16
  Its square root	4
  To the same added the 2 from the first line	6

  I say that 6 is the sought-for fourth proportional term.

Here is his geometrical proof:

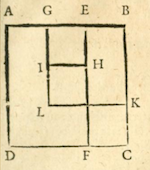
Figure from Stevin, L'Arithmétique p. 267. With modern notation: Stevin starts with a square ABCD representing $x^2$, so its side BC has length $x$. He draws EF parallel to AD, with AE $= 4$. So the rectangle ADFE measures $4x$ and then the rectangle EFCB has area $x^2-4x = 12$. Pick G the midpoint of AE, and draw the square GLKB.
    The rest of the argument as it appears in L'Arithmétique:

Half of AE $=4$ which is GE	2
Its square GEHI	4
Add to the same the given ${\bf 0}$, i.e. EFCB	12
Gives sum for the gnomon HIGBCF
or for the square GBKL of same area	16
Its root BK	4
Add to the same GE$=2$ or instead KC = GE, makes for BC	6
Q.E.D. [My translations -TP]

• $z^2=az + b^2$
• $y^2=-ay + b^2$
• $z^2 = az-b^2$.

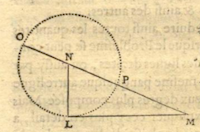
Cases 1 and 2. "I construct the right triangle NLM with one leg $LM$ equal to $b$, and the other $LN$ is $\frac{1}{2}a$, half of the other known quantity which was multiplied by $z$, which I suppose to be the unknown length; then extending $MN$, the hypothenuse of this triangle, to the point $O$, such that $NO$ is equal to $NL$, the entirety $OM$ is the sought-for length; and it can be expressed in this way: $$z=\frac{1}{2}a + \sqrt{\frac{1}{4}aa + bb}.$$ Whereas if I have $yy=-ay+bb$, with $y$ the unknown quantity, I construct the same right triangle $NLM$, and from the hypothenuse $MN$ I subtract $NP$ equal to $NL$, and the remainder $PM$ is $y$, the sought-for root. So that I have $y=-\frac{1}{2}a + \sqrt{\frac{1}{4}aa + bb}."$

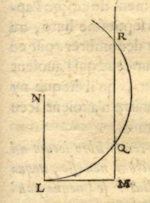
Case 3. "Finally, if I have $$z^2=az-bb$$ I draw $NL$ equal to $\frac{1}{2}a$ and $LM$ equal to $b$, as before; then, instead of joining the points $MN$, I draw $MQR$ parallel to $LN$, and having drawn a circle with center $N$ which cuts it at the points $Q$ and $R$, the sought-for length is $MQ$, or $MR$; since in this case it can be expressed two ways, to wit, $z=\frac{1}{2}a + \sqrt{\frac{1}{4}aa - bb}$ and $z=\frac{1}{2}a - \sqrt{\frac{1}{4}aa - bb}.$ And if the circle, which has its center at $N$ and passes through $L$ neither cuts nor touches the straight line $MQR$, the equation has no root, so one can state that the construction of the proposed problem is impossible." [My translation. Checking Descartes' constructions involves some standard Euclidean geometry.-TP]

• "Consider the equation $xx+2ax = bb$; add to one and to the other sides the square of half the coefficient of the second term, i.e. $aa$, and it becomes $xx+2ax+aa = aa + bb$ and, extracting the root, $x=\pm\sqrt{aa+bb} -a$."

But when Agnesi comes to a general treatment she follows Descartes, using identical geometric constructions, with one significant improvement, as implied above: negative roots are calculated and given the same status as positive ones:

• "Negative values, which are still called false, are no less real than the positive, and have the only difference, that if in the solution to the problem the positives are taken from the fixed starting point of the unknown toward one side, the negatives are taken from the same point in the opposite direction."

• MP and $-$MO as roots of $xx+ax-bb=0$
• MO and $-$MP as roots of $xx-ax-bb=0$
• $-$MQ and $-$MR as roots of $xx+ax+bb=0$
• MQ and MR as roots of $xx-ax+bb=0$.

• §145. "But notwithstanding [their being impossible] these numbers present themselves to the mind; they exist in our imagination, and we still have a sufficient idea of them; since we know that by $\sqrt{-4}$ is meant a number which, multiplied by itself, produces $-4$; for this reason also, nothing prevents us from making use of these imaginary numbers, and employing them in calculation."

• §700. "A very remarkable case sometimes occurs, in which both values of $x$ become imaginary, or impossible; and it is then wholly impossible to assign any value for $x$, that would satisfy the terms of the equation."

In 20th century physics

A Gaussian function $f(x)=C\exp(-\frac{1}{2}ax^2)$ corresponds to a familiar "bell-shaped curve." In multivariable calculus we learn that $\int_{-\infty}^{\infty}\,f(x)\,dx=C\sqrt{\frac{2\pi}{a}}$; this also holds for $\int_{-\infty}^{\infty}\,f(x-\mu)\,dx$, with $\mu$ any finite number.

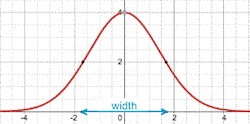
The width of the Gaussian $f(x)=C\exp(-\frac{1}{2}ax^2)$, defined as the distance between the two points where $\,f=\frac{C}{2}$, can be calculated to be  $2\sqrt{\frac{2\ln 2}{a}}$. In this image with $C=4$, $a=\frac{1}{2}$, the width is 3.33. Note that the width does not depend on the factor $C$.

The Fourier transform of $f$ (taking $C=1$) is the function $${\hat f}(y)= \int_{-\infty}^{\infty}\exp(ixy)\,f(x)~dx = \int_{-\infty}^{\infty}\exp(-\frac{1}{2}ax^2 + ixy)~dx.$$ This integral can be computed by completing the square: write $-\frac{1}{2}ax^2 + ixy$ as $-\frac{1}{2}a(x^2 -\frac{2iyx}{a} +\frac{y^2}{a^2}-\frac{y^2}{a^2})= -\frac{1}{2}a (x-\frac{iy}{a})^2 - \frac{y^2}{2a}$. Then $$ {\hat f}(y)= \int_{-\infty}^{\infty}\exp(-\frac{y^2}{2a})\,\exp\left (-\frac{1}{2}a(x-\frac{iy}{a})^2\right )\,dx=\sqrt{\frac{2\pi}{a}}\,\exp(-\frac{y^2}{2a}).$$ This means that the Fourier transform of $f$ is again a Gaussian; the parameter $a$ has become $\frac{1}{a}$, so the product of the widths of $\,f$ and its Fourier transform ${\,\hat f}$ is constant. The wider $\,f$ is, the narrower ${\,\hat f}$ must be, and vice-versa. This phenomenon is the mathematical form of the uncertainty principle.