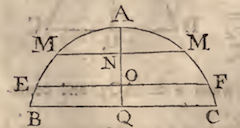
 EXAMPLE IX. Let it be proposed to find the Area of a Semi-circle
AREH.
EXAMPLE IX. Let it be proposed to find the Area of a Semi-circle
AREH.
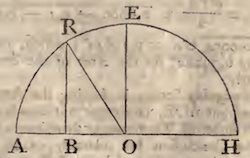
Here, putting the Diameter AH $=a$, AB $=x$, and BR $=y~$ &c.
(as usual) we have $y^2$ (BR$^2$) $=ax-xx$ (AB$\times$BH),
and consequently $\dot{u}$ ($y\dot{x}$) $=\dot{x}\sqrt{ax-xx}$
$=\displaystyle{ a^{\frac{1}{2}} x^{\frac{1}{2}} \dot{x}\times
\overline{1-\frac{x}{a}}^{\frac{1}{2}}}:$ Which Expression not
being of the Kind [described previously], that admit of Fluents in
finite Terms, let it be therefore resolved into an Infinite Series
and you will have
$\displaystyle{\dot{u} = a^{\frac{1}{2}} x^{\frac{1}{2}} \dot{x}\times
\overline{1-\frac{x}{2a}-\frac{x^2}{8a^2}-\frac{x^3}{16a^3}
-\frac{5x^4}{128a^4}}}~$ &c.
$\displaystyle{
=a^{\frac{1}{2}}\times \overline{
x^{\frac{1}{2}}\dot{x}
-\frac{x^{\frac{3}{2}}}{2a}\dot{x}
-\frac{x^{\frac{5}{2}}}{8a^2}\dot{x}
-\frac{x^{\frac{7}{2}}}{16a^3}\dot{x}}}~$
&c.
From whence, the Fluent of every Term being taken, according to
the common Method, there will come out
$u =\displaystyle{=a^{\frac{1}{2}}\times \overline{ \frac{2x^{\frac{3}{2}}}{3}
-\frac{x^{\frac{5}{2}}}{5a} -\frac{x^{\frac{7}{2}}}{28a^2}
-\frac{x^{\frac{9}{2}}}{72a^3} -\frac{5x^{\frac{11}{2}}}{704a^4}}}~$&c.
$=\displaystyle{x\sqrt{ax}\times
\overline{ \frac{2}{3}
-\frac{x}{5a} -\frac{x^2}{28a^2}
-\frac{x^3}{72a^3} -\frac{5x^4}{704a^4}}}~$&c.
= the Area ABR. Now, when $x=\frac{1}{2}a$, the Ordinate BR
will coincide with the Radius OE; in which Case the Area becomes
$=\frac{1}{2}a\sqrt{\frac{1}{2}aa}\times
\overline{ \frac{2}{3}
-\frac{1}{10} -\frac{1}{112}
-\frac{1}{576} -\frac{5}{11264}
}~$&c.
$=\displaystyle{\frac{a^2\sqrt{\frac{1}{2}}}{2}\times
\overline{0,6666-0,1-0,0089-0,0017-0,0004
}}~$&c. $=0,1964a^2$; which, when
multiplied by 2, gives $0,3928a^2$ for the Area
of the Semi-circle AEH, nearly.
|
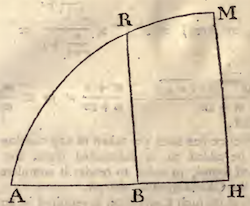 EXAMPLE II. Let the Curve ARMH, whose Area you would find,
be the common
Parabola.
EXAMPLE II. Let the Curve ARMH, whose Area you would find,
be the common
Parabola. EXAMPLE IX. Let it be proposed to find the Area of a Semi-circle
AREH.
EXAMPLE IX. Let it be proposed to find the Area of a Semi-circle
AREH.
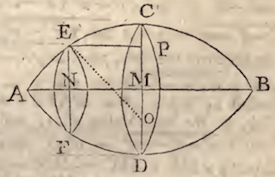 EXAMPLE VII. Where it is required to find the Content of a
Parabolic Spindle; generated by the rotation of a given
Parabola ACB about its ordinate AB.
EXAMPLE VII. Where it is required to find the Content of a
Parabolic Spindle; generated by the rotation of a given
Parabola ACB about its ordinate AB.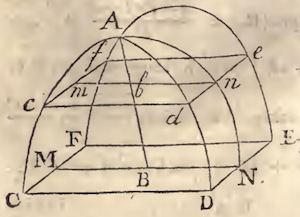
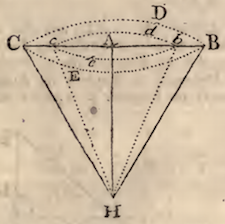
 EXAMPLE IV. [Center of Gravity = O] Let ABC represent a Segment of a Sphere, or Spheroid.
EXAMPLE IV. [Center of Gravity = O] Let ABC represent a Segment of a Sphere, or Spheroid.
 PROB I. Supposing AC perpendicular to AB,
and that a Corpuscle at C is
attracted twards every Point or Particle of the Line AB, by Forces in the
reciprocal duplicate Ratio of the Distances; to determine the Ratio of
the whole Force whereby the Corpuscle is urged in the Direction CA.
PROB I. Supposing AC perpendicular to AB,
and that a Corpuscle at C is
attracted twards every Point or Particle of the Line AB, by Forces in the
reciprocal duplicate Ratio of the Distances; to determine the Ratio of
the whole Force whereby the Corpuscle is urged in the Direction CA.
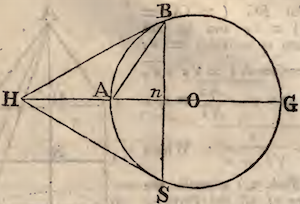 PROB. V. The Law of the Force being still supposed the same,
to determine
the attraction of a Sphere OABGS, at any given point H above its
Surface.
PROB. V. The Law of the Force being still supposed the same,
to determine
the attraction of a Sphere OABGS, at any given point H above its
Surface.