A musical score has basically two dimensions: pitch and time. In a one-voice musical text, for example, the pitch (corresponds to frequency) of a note is represented vertically, and performance time runs from left to right.

In this line from from the Kyrie eleison in a 14th-15th century chantbook, time runs from left to right and pitch corresponds to height. Many details of musical notation have changed since those times, but the basic principles are exactly the same. This image, and the image of the full text, are used by permission of the University of Missouri-Kansas City Libraries, Dr. Kenneth J. LaBudde Department of Special Collections.
So topologically a one-voice musical score is a 2-dimensional strip. The horizontal (time) coordinate runs from start to finish; the vertical coordinate runs from lower pitches to higher pitches. In the chantbook score above, the clef at the start indicates that the second line in the staff corresponds to "fa" on the musical scale.
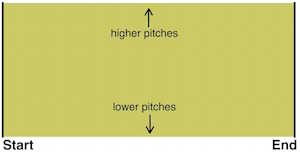
A one-voice musical score as a rectangular strip.
When a score has symmetry, the topology becomes more interesting. Suppose the score repeats: plays the same sequence of notes over and over. This happens, for example, with a vamp, a sequence of notes or chords played repeatedly as an accompaniment or just to fill time while waiting for something to start. In music notation, the repeat bars identify the end of the sequence with the beginning. This identification makes the score, topologically, into a cylinder.
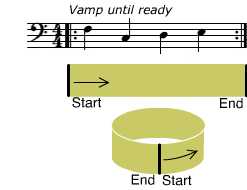
An elementary vamp score is topologically a cylinder.
A (2-part) canon is a score in which a second voice imitates the first voice after a delay. One of the best known is Frère Jacques. The tune is 8 measures long. In measure 3 a second voice starts repeating what the first voice sang. The two voices fit together musically (they "harmonize"); the harmony continues through measures 9 and 10, where the first voice starts over as the second voice is finishing. Then the second voice comes in again, and the sequence from bar 3 through 10 forms a steady state that naturally repeats over and over.

Frère Jacques. Since the first voice starts up again while the second voice is finishing, there is no natural ending point: the the steady state (blue box) can be repeated as often as wished.
Canons were a speciality of the great Baroque composer Johann Sebastian Bach (1685-1750). In fact the best picture we have of him shows him holding the score of a canon, the thirteenth from the set of 14 he entitled "Fourteen Canons on the first eight fundamental notes of the aria [from the Goldberg Variations]".

In the 1746 portrait by Elias Gottlob Haussmann, Bach is holding a copy of Canon 13 from his set of 14 canons on the first eight notes of the Goldberg Variations ground, BWV 1087. Image in public domain, via Wikimedia Commons.
This set of canons has its own story. Except for two of them, the one in the painting and another that Bach had written in a friend's autograph book, its existence was unknown until 1974. That's when it was discovered, written in the back of what turned out to be Bach's own copy of the Goldberg Variations. We will be analyzing two others from the set, Canons 3 and 5.
Canons 3, 4 and 5 all involve a voice and its inversion, where all the intervals are reversed, moving down when the original moves up, and vice-versa (Bach describes them as motu recto et contrario). In Canon 3, the leading voice plays the first eight notes of the Goldberg ground, while the follower, starting in measure 3, plays the same melody upside-down.
![]()

Top: the first eight notes of the theme of the Goldberg Variations. Center: the same score, reflected up; the axis of symmetry is between B and middle C. Bottom, the two voices together. The first voice starts over while the second is only half done, so the steady state of the canon naturally repeats.
Topologically, both Frère Jacques and BWV 1087, Canon 3 have the same structure: after the introductory measures, the canon settles into a cylindrical steady state. All of Bach's canons are organized this way.
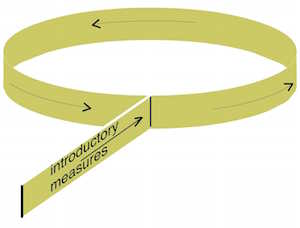
The general topology of a Bach canon.

Canon 5 on the Goldberg ground. In both canons, the follower comes in halfway through the leader's statement. The blue box shows the steady state.
Let us focus on the top two voices, in the steady state, and compare the score with its mirror image (flipped down). The last two measures of the score can be seen to be identical to the first two measures upside down (orange boxes in the image), and vice-versa. The score has glide-reflection symmetry.

The score of the top voices of Canon 5 (steady state) has glide-reflection symmetry. (Tails on notes go up on the right and down on the left; this property gets reversed in the mirror).
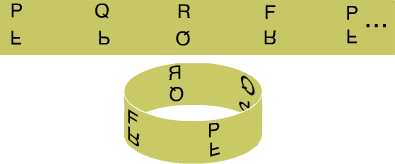
Any periodic text with glide-reflection symmetry can be encoded on a Möbius strip:
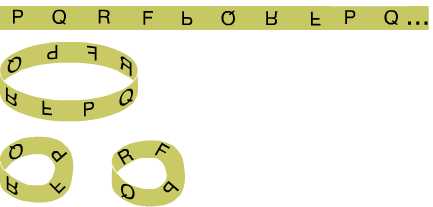
A periodic text with glide-reflection symmetry, encoded on a Möbius strip. The strip is shown from above and below.
Since the score of the two upper voices of Canon 5 has glide-reflection symmetry, we can apply this process to it:

The score of the two upper voices of Canon 5 printed on a cylinder.

The cylinder wrapped twice on itself, with a twist, to form a Möbius strip. Note that the two copies of each note now match exactly (except for their tails).
The sound of a Möbius strip.
The score for the lower two voices also has glide-reflection symmetry: it also can be encoded on a Möbius strip, but on a different one, because the axes of symmetry are different.
Note that the score of a canon in contrary motion does not necessarily have glide-reflection symmetry. If a glide-reflection symmetry is repeated, it leads back to the original state. A canon in contrary motion only has this property if the second voice comes exactly at the halfway point.
This periodic "2-voice" text displays imitation in contrary motion but does not have glide-reflection symmetry.
Our Canons 3 and 5 from BWV 1087 have this property: their steady states can be read from Möbius strips. Other Bach contrary-motion canons, for example Canons 3 and 9 from the Musical Offering, do not have this property, nor do Variations 12 and 15 from the Goldberg set. This corrects an erroneous statement in our Musical Times article, where we stated that they did.
A beautiful video has been posted on YouTube showing that Bach's "Crab Canon" (Canon 1 from the Musical Offering) can be read from a Möbius strip. In the Crab Canon, the follower plays the leader backwards, from finish to start. This is an amazing piece of music, but it really has nothing to do with a Möbius strip. The flaw in the construction is that the score ends up written on both sides of a Möbius strip, so it is really written on the connected double cover of the Möbius strip, i.e. a cylinder. Any repeating text can be so represented.